2016-2017学年湖南省邵阳市武冈市九年级下学期期中数学试卷
试卷更新日期：2017-05-25 类型：期中考试
一、选择题
-
1. ﹣ 的相反数是（ ）A、 B、﹣ C、﹣ D、2. 下列“表情”中属于轴对称图形的是（ ）A、
B、
C、
D、
3. 如图，∠1=∠B，∠2=20°，则∠D=（ ）
A、20° B、22° C、30° D、45°4. 一次函数y=﹣2x+3的图象不经过的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 学校“清洁校园”环境爱护志愿者的年龄分布如图，那么这些志愿者年龄的众数是（ ）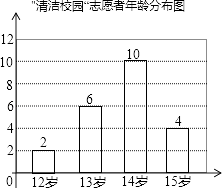
A、12岁 B、13岁 C、14岁 D、15岁6. 将分式方程 = 去分母后得到的整式方程，正确的是（ ）A、x﹣2=2x B、x2﹣2x=2x C、x﹣2=x D、x=2x﹣47. 一元二次方程5x2﹣11x+4=0的根的情况是（ ）A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根8. 如图，在Rt△ABC中，∠ACB=90°，D、E分别为AC、AB的中点，连DE、CE．则下列结论中不一定正确的是（ ）
A、ED∥BC B、ED⊥AC C、∠ACE=∠BCE D、AE=CE9. 如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是 上不与点A、点C重合的一个动点，连接AD、CD，若∠APB=80°，则∠ADC的度数是（ ）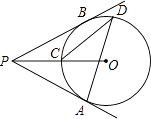
A、15° B、20° C、25° D、30°10.下面每个表格中的四个数都是按相同规律填写的：
根据此规律确定x的值为（ ）
A、135 B、170 C、209 D、252二、填空题
-
11. 分解因式：2x2﹣8= ．12. 要从甲、乙两名运动员中选出一名参加“2016里约奥运会”100m比赛，对这两名运动员进行了10次测试，经过数据分析，甲、乙两名运动员的平均成绩均为10.05（s），甲的方差为0.024（s2），乙的方差为0.008（s2），则这10次测试成绩比较稳定的是运动员．（填“甲”或“乙”）13. 如图，△ABC绕点A顺时针旋转80°得到△AEF，若∠B=100°，∠F=50°，则∠α的度数是 ．
14. 写出一个图象位于二、四象限的反比例函数的表达式，y= ．15. 不等式组 的解集为 ．16. 据统计，2014年我国高新技术产品出口总额达40570亿元，将数据40570亿用科学记数法表示为亿元．17. 如图，在平行四边形ABCD中，点E、F分别在边BC、AD上，请添加一个条件 ， 使四边形AECF是平行四边形（只填一个即可）．
18. 如图，四个小正方形的边长都是1，若以O为圆心，OG为半径作弧分别交AB、DC于点E、F，则图中阴影部分的面积为 ．
三、解答题
-
19. 计算：（ ﹣1）0+（﹣3）2﹣2sin60°．20. 先化简下面代数式，再求值：（x+2）（x﹣2）+x（3﹣x），其中x=+1．21. 已知：E、F是▱ABCD的对角线AC上的两点，AF=CE，求证：∠CDF=∠ABE．
22. 如图1是一个新款水杯，水杯不盛水时按如图2所示的位置放置，这样可以快速晾干杯底，干净透气；将图2的主体部分的抽象成图3，此时杯口与水平直线的夹角35°，四边形ABCD可以看作矩形，测得AB=10cm，BC=8cm，过点A作AF⊥CE，交CE于点F．
(1)、求∠BAF的度数；（sin35°≈0.5736，cos35°≈0.8192，tan35°≈0.7002）(2)、求点A到水平直线CE的距离AF的长（精确到0.1cm）23. 因市场竞争激烈，国商进行促销活动，决定对学习用品进行打八折出售，打折前，买2本笔记本和1支圆珠笔需要18元，买1本笔记本和2支圆珠笔需要12元．(1)、求打折前1本笔记本，1支圆珠笔各需要多少元．(2)、在促销活动时间内，购买50本笔记本和40支圆珠笔共需要多少元？24. 为推广阳光体育“大课间”活动，某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目，为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：
(1)、在这项调查中，共调查了多少名学生？(2)、请计算喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；(3)、若调查到喜欢“跳绳”的4名学生中有2名男生，2名女生．现从这4名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．25.阅读理解：
(1)、如图（1），等边△ABC内有一点P到顶点A，B，C的距离分别为3，4，5，则∠APB= ．分析：由于PA，PB不在一个三角形中，为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌ ， 这样，就可以利用全等三角形知识，将三条线段的长度转化到一个三角形中从而求出∠APB的度数．
(2)、请你利用第（1）题的解答思想方法，解答下面问题：已知如图（2），△ABC中，∠CAB=90°，AB=AC，E、F为BC上的点且∠EAF=45°，求证：BE2+CF2=EF2 ．26.如图，在平面直角坐标系xOy中，直线y=x+3交x轴于A点，交y轴于B点，过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C，点D是抛物线的顶点．
(1)、求此抛物线的解析式；(2)、点P是直线AB上方的抛物线上一点，（不与点A、B重合），过点P作x轴的垂线交x轴于点H，交直线AB于点F，作PG⊥AB于点G．求出△PFG的周长最大值；(3)、在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M，使得△ABM与△ABD的面积相等？若存在，请求出此时点M的坐标；若不存在，请说明理由．