2016-2017学年广东省汕头市澄海区九年级上学期期末数学试卷
试卷更新日期：2017-05-25 类型：期末考试
一、选择题
-
1. 若二次函数y=ax2的图象经过点P（﹣2，4），则该图象必经过点（ ）A、（4，﹣2） B、（﹣4，2） C、（﹣2，﹣4） D、（2，4）2. 一元二次方程x2﹣8x﹣1=0配方后可变形为（ ）A、（x+4）2=17 B、（x﹣4）2=17 C、（x+4）2=15 D、（x﹣4）2=153. 随着人们生活水平的提高，我国拥有汽车的居民家庭也越来越多，下列汽车标志中，是中心对称图形的是（ ）A、
B、
C、
D、
4. 如图，经过原点O的⊙P与x、y轴分别交于A、B两点，点C是劣弧OB上一点，则∠ACB=（ ）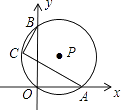
A、80° B、90° C、100° D、无法确定5. 在二次函数y=x2﹣2x+3的图象中，若y随x的增大而增大，则x的取值范围是（ ）A、x＜﹣1 B、x＞﹣1 C、x＜1 D、x＞16. 有x支球队参加篮球比赛，共比赛了21场，每两队之间都比赛一场，则下列方程中符合题意的是（ ）A、x（x﹣1）=21 B、x（x+1）=21 C、x（x﹣1）=42 D、x（x+1）=427. 三张外观相同的卡片分别标有数字1、2、3，从中随机一次抽出两张，这两张卡片上的数字恰好都小于3的概率是（ ）A、 B、 C、 D、8. 如果将抛物线y=x2+2先向左平移1个单位，再向下平移2个单位，那么所得新抛物线的表达式是（ ）A、y=（x﹣1）2 B、y=（x+1）2 C、y=x2+1 D、y=x2+39. 如图，在△ABC中，∠CAB=65°，在同一平面内，将△ABC绕点A按逆时针方向旋转到△AB'C'的位置，使得CC'∥AB，则∠BAB'=（ ）
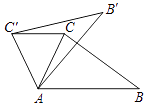A、30° B、35° C、40° D、50°10. 如图，在扇形OAB中，∠AOB=90°，正方形CDEF的顶点C是弧AB的中点，点D在OB上，点E在OB的延长线上，若正方形CDEF的边长为2，则图中阴影部分的面积为（ ）
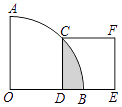A、π﹣2 B、2π﹣2 C、4π﹣4 D、4π﹣8二、填空题
-
11. 点P（2，﹣3）关于原点的对称点P′的坐标为 ．12. 一元二次方程x2﹣16=0的解是 ．13. 抛物线y=x2+2x+1的顶点坐标是 ．14. 若⊙O是等边△ABC的外接圆，⊙O的半径为2，则等边△ABC的边长为 ．
15. 用一根长为16cm的铁丝围成一个矩形，则围成矩形面积的最大值是cm2 ．16. 已知正方形ABCD中，点E在边DC上，DE=2，EC=1（如图所示）把线段AE绕点A旋转，使点E落在直线BC上的点F处，则F、C两点的距离为 ．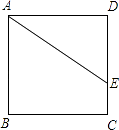
三、解答题
-
17. 设二次函数的图象的顶点坐标为（﹣2，2），且过点（1，1），求这个函数的关系式．18. 已知x=﹣1是关于x的方程x2+2ax+a2=0的一个根，求a的值．19. 在数学活动课中，同学们准备了一些等腰直角三角形纸片，从每张纸片中剪出一个扇形制作圆锥玩具模型．如图，已知△ABC是腰长为4的等腰直角三角形．
(1)、在等腰直角三角形ABC纸片中，以C为圆心，剪出一个面积最大的扇形（要求：尺规作图，保留作图痕迹，不写作法）；(2)、请求出所制作圆锥底面的半径长．20. 小明、小林是三河中学九年级的同班同学，在四月份举行的自主招生考试中，他俩都被同一所高中提前录取，并将被编入A、B、C三个班，他俩希望能再次成为同班同学．(1)、请你用画树状图法或列举法，列出所有可能的结果；(2)、求两人再次成为同班同学的概率．21. 已知关于的方程x2+2x+m﹣2=0．(1)、若该方程有两个不相等的实数根，求实数m的取值范围；(2)、当该方程的一个根为1时，求m的值及方程的另一根．22. 在某市组织的大型商业演出活动中，对团体购买门票实行优惠，决定在原定票价基础上每张降价80元，这样按原定票价需花费6000元购买的门票张数，现在只花费了4800元．(1)、求每张门票的原定票价；(2)、根据实际情况，活动组织单位决定对于个人购票也采取优惠政策，原定票价经过连续二次降价后降为324元，求平均每次降价的百分率．23. 如图，△ABC中，AB=AC=1，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE、CF相交于点D．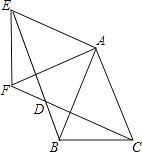
(1)、求证：BE=CF；(2)、当四边形ACDE为菱形时，求BD的长．24. 如图，已知AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE．
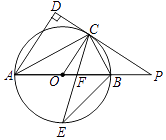(1)、求证：AC平分∠DAB；(2)、求证：△PCF是等腰三角形；(3)、若AF=6，EF=2 ，求⊙O 的半径长．25.如图，已知抛物线y=ax2+bx+c（a≠0）的顶点坐标为Q（2，﹣1），且与y轴交于点C（0，3），与x轴交于A、B两点（点A在点B的右侧），点P是该抛物线上一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥y轴，交AC于点D．
(1)、求该抛物线的函数关系式；(2)、设P（x，y），PD的长度为l，求l与x的函数关系式，并求l的最大值；(3)、当△ADP是直角三角形时，求点P的坐标．