浙江省绿色联盟2019届高三5月适应性考试数学试题
试卷更新日期:2019-05-31 类型:高考模拟
一、选择题:本大题共有10小题,每小题4分,共40分。
-
1. 复数z1=2-i,z2=1+2i,i为虚数单位,则z1· =( )
A、4-5i B、3i C、4-3i D、-5i2. 已知x,y为实数,则“xy≥0”是|x+y|≥|x-y|的( )A、充分不必要条件 B、必要不充分条件 C、充分且必要条件 D、既不充分也不必要条件3. 已知a为第二象限角,且3sina+cosa=0,则sina=( )A、 B、 C、- D、-4. 设U为全集,对于集合M,N,下列集合之间关系不正确的是( )A、M∩N MUN B、(CUM)U(CUN)=CU(M∩N) C、(CUM) ∩(CUN)=CU(MUN) D、(CUM) ∩(CUN)=CU(M∩N)5. 已知函数f(x)图象如图所示,则该图象所对应的函数是( )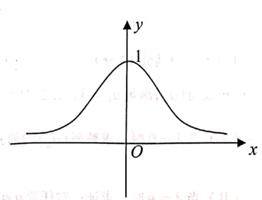 A、f(x)=e-x B、f(x)=e-2 C、f(x)=ex2 D、f(x)=e-x26. 已知实数x,y满足不等式组 ,则点(x,y)构成平面区域的面积是( )A、3 B、 C、2 D、7. 在三棱锥P-ABC中,E为线段AB(不包括端点)上一点,则错误的是( )A、一定存在唯一的平面a经过点E,使得平面a∥平面PAC B、一定存在唯一的平面a经过点E,使得平面a⊥平面PAC C、一定存在唯一的平面a经过点E,使得平面a⊥PA D、在平面ABC内,一定存在唯一的直线l经过点E,使得l∥平面PAC8. 安排3人完成5项不同工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式种数为( )A、60 B、150 C、180 D、2409. 已知a= ,b= ,c= ,则( )A、a>b>c B、c>a>b C、a>c>b D、c>b>a10. 在矩形ABCD中,AB=1,AD=2,动点P在以C为圆心且与BD相切的圆上,若 ,设λ+2μ的最大值为M,最小值为N,则M-N的值为( )
A、f(x)=e-x B、f(x)=e-2 C、f(x)=ex2 D、f(x)=e-x26. 已知实数x,y满足不等式组 ,则点(x,y)构成平面区域的面积是( )A、3 B、 C、2 D、7. 在三棱锥P-ABC中,E为线段AB(不包括端点)上一点,则错误的是( )A、一定存在唯一的平面a经过点E,使得平面a∥平面PAC B、一定存在唯一的平面a经过点E,使得平面a⊥平面PAC C、一定存在唯一的平面a经过点E,使得平面a⊥PA D、在平面ABC内,一定存在唯一的直线l经过点E,使得l∥平面PAC8. 安排3人完成5项不同工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式种数为( )A、60 B、150 C、180 D、2409. 已知a= ,b= ,c= ,则( )A、a>b>c B、c>a>b C、a>c>b D、c>b>a10. 在矩形ABCD中,AB=1,AD=2,动点P在以C为圆心且与BD相切的圆上,若 ,设λ+2μ的最大值为M,最小值为N,则M-N的值为( )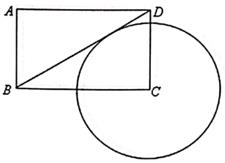 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共7小题,11-14每空3分,15-17每小题4分,共36分)
-
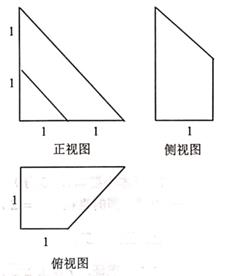
11. 已知函数f(x)=aex+|x|+a-1为偶函数,则实数a=:关于x的不等式|f(x)|≤0的解为 .12. 已知点M为双曲线x2- =1左支上一动点,右焦点为F,点N(0,6),则该双曲线的离心率为: ;|MN|+|MF|的最小值为 .13. 已知随机变量ξ满足P(ξ=i)= (i=1,2,3),则E(ξ)=;D(ξ)= .14. 在△ABC中,角A,B,C所对的边分别为a,b,c,若a2+c2-b2+2bccosA-2c=0,c cosA=b(1-cosC),且C= ,则c=;△ABC的面积S= .15. 如图是某几何体的三视图,则该几何体的体积为 .
 16. 如图,在宽8米的矩形教室MEFN正前方有一块长6米的黑板AB,学生座位区域CEFD距黑板最近1米,在教室左侧边CE上寻找黑板AB的最大视角点P(即使∠APB最大),则CP=时,∠APB最大.
16. 如图,在宽8米的矩形教室MEFN正前方有一块长6米的黑板AB,学生座位区域CEFD距黑板最近1米,在教室左侧边CE上寻找黑板AB的最大视角点P(即使∠APB最大),则CP=时,∠APB最大.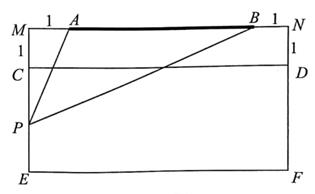 17. 已知数列{an}满足an+1+(-1)nan=n(n∈N*),记数列{an}的前n项和为Sn , 则S60= .
17. 已知数列{an}满足an+1+(-1)nan=n(n∈N*),记数列{an}的前n项和为Sn , 则S60= .三、解答题(本大题共5小题,共74分)
-
18. 已知函数f(x)=sinxsin( -x)- cos2x.
(Ⅰ)求f( )的值:
(Ⅱ)求f(x)的单调区间。
19. 如图,圆的直径AC=2,B为圆周上不与点A,C重合的点,PA垂直于圆所在的平面,∠PCA=45°.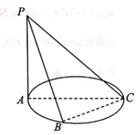
(Ⅰ)求证:PB⊥BC;
(Ⅱ)若BC= ,求二面角B-PC-A的余弦值.
20. 已知数列{an}满足a1=3,n≥2时,an-2an-1=λ×3n .(Ⅰ)当λ=0时,求数列{an}的前n项和Sn:
(Ⅱ)当λ=n时,求证:对任意n∈N*, 为定值。