2016-2017学年江苏省苏州市高新区八年级下学期期中测试数学试卷
试卷更新日期:2017-05-24 类型:期中考试
一、选择题
-
1. 小明3分钟共投篮80次,进了50个球,则小明进球的频率是( )
A、80 B、50 C、1.6 D、0.6252. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 =2 D、4. 已知平行四边形ABCD中,∠B=4∠A,则∠C=( )A、18° B、36° C、72° D、144°5. 如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
3. 下列计算正确的是( )A、 B、 C、 =2 D、4. 已知平行四边形ABCD中,∠B=4∠A,则∠C=( )A、18° B、36° C、72° D、144°5. 如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= AM2 .
其中正确结论的个数是( )
 A、1 B、2 C、3 D、46.
A、1 B、2 C、3 D、46.= .
7. 若反比例函数y= 图象经过点A(﹣ , ),则k= .8.如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,平行四边形ABCD的周长为40.则平行四边形ABCD的面积为 .
 9. 如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1 , 然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2 , 再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3 , …,已知AB=6, BC=8,按此方法得到的四边形A5B5C5D5的周长为 .
9. 如图,顺次连接矩形ABCD四边的中点得到四边形A1B1C1D1 , 然后顺次连接四边形A1B1C1D1的中点得到四边形A2B2C2D2 , 再顺次连接四边形A2B2C2D2四边的中点得到四边形A3B3C3D3 , …,已知AB=6, BC=8,按此方法得到的四边形A5B5C5D5的周长为 . 10.
10.如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为.
 11. 为了解某市参加中考的32000名学生的体质情况,抽查了其中1600名学生的体重进行统计分析.下面叙述正确的是( )A、32000名学生是总体 B、1600名学生的体重是总体的一个样本 C、每名学生是总体的一个个体 D、以上调査是普查12. 函数y=kx+1与函数y= 在同一坐标系中的大致图象是( )A、
11. 为了解某市参加中考的32000名学生的体质情况,抽查了其中1600名学生的体重进行统计分析.下面叙述正确的是( )A、32000名学生是总体 B、1600名学生的体重是总体的一个样本 C、每名学生是总体的一个个体 D、以上调査是普查12. 函数y=kx+1与函数y= 在同一坐标系中的大致图象是( )A、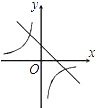 B、
B、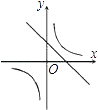 C、
C、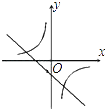 D、
D、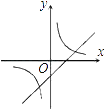 13. 在平面中,下列说法正确的是( )A、四边相等的四边形是正方形 B、四个角相等的四边形是矩形 C、对角线相等的四边形是菱形 D、对角线互相垂直的四边形是平行四边形14. 已知点P(x1 , ﹣2)、Q(x2 , 2)、R(x3 , 3)三点都在反比例函数y= 的图象上,则下列关系正确的是( ).A、x1<x3<x2 B、x<1x2<x3 C、x3<x2<x1 D、x2<x3<x115. 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=﹣ 的图象上,若点A的坐标为(﹣2,﹣2),则k的值为( )
13. 在平面中,下列说法正确的是( )A、四边相等的四边形是正方形 B、四个角相等的四边形是矩形 C、对角线相等的四边形是菱形 D、对角线互相垂直的四边形是平行四边形14. 已知点P(x1 , ﹣2)、Q(x2 , 2)、R(x3 , 3)三点都在反比例函数y= 的图象上,则下列关系正确的是( ).A、x1<x3<x2 B、x<1x2<x3 C、x3<x2<x1 D、x2<x3<x115. 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=﹣ 的图象上,若点A的坐标为(﹣2,﹣2),则k的值为( ) A、4 B、﹣4 C、8 D、﹣8
A、4 B、﹣4 C、8 D、﹣8二、填空题
-
16. 在函数 中,自变量x的取值范围是.17. 如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是度.
 18. 如图,在四边形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
18. 如图,在四边形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
三、解答题.
-
19. 计算题
(Ⅰ) ;(Ⅱ) .
20. 2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:
(Ⅰ)本次调查共选取名居民;
(Ⅱ)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(Ⅲ)如果该社区共有居民1600人,估计有多少人从不闯红灯?
21.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(Ⅰ)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(Ⅱ)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
 22. 已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
22. 已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.(Ⅰ)求证:四边形AODE是矩形;
(Ⅱ)若AB=6,∠BCD=120°,求四边形AODE的面积.
 23. 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
23. 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:(Ⅰ)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(Ⅱ)求图中t的值;
(Ⅲ)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?
 24. 如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
24. 如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.(Ⅰ)求证:MD和NE互相平分;
(Ⅱ)若BD⊥AC,EM=2 ,OD+CD=7,求△OCB的面积.
 25. 如图,一次函数y=kx+b与反比例函数 的图象交于A(m,6),B(3,n)两点.
25. 如图,一次函数y=kx+b与反比例函数 的图象交于A(m,6),B(3,n)两点.(Ⅰ)求一次函数的解析式;
(Ⅱ)根据图象直接写出 的x的取值范围;
(Ⅲ)求△AOB的面积.
 26. 已知:直线l1与直线l2平行,且它们之间的距离为2,A、B是直线l1上的两个定点,C、D是直线l2上的两个动点(点C在点D的左侧),AB=CD=5,连接AC、BD、BC,将△ABC沿BC折叠得到△A1BC.
26. 已知:直线l1与直线l2平行,且它们之间的距离为2,A、B是直线l1上的两个定点,C、D是直线l2上的两个动点(点C在点D的左侧),AB=CD=5,连接AC、BD、BC,将△ABC沿BC折叠得到△A1BC.(Ⅰ)求四边形ABDC的面积.
(Ⅱ)当A1与D重合时,四边形ABDC是什么特殊四边形,为什么?
(Ⅲ)当A1与D不重合时:①连接A1、D,求证:A1D∥BC;②若以A1 , B,C,D为顶点的四边形为矩形,且矩形的边长分别为a,b,求(a+b)2的值.
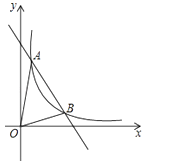
 27. 六•一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A、B、C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1、S2、S3 , 并测得S2=6(单位:平方米).OG=GH=HI.
27. 六•一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A、B、C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1、S2、S3 , 并测得S2=6(单位:平方米).OG=GH=HI.(Ⅰ)求S1和S3的值;
(Ⅱ)设T(x,y)是弯道MN上的任一点,写出y关于x的函数关系式;
(Ⅲ)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
