广东省深圳市七校联合体2019届高三理数冲刺模拟试卷
试卷更新日期:2019-05-29 类型:高考模拟
一、选择题:本大题共12个小题,每小题5分,共60分.
-
1. 已知 为实数集,集合 ,则 ( )A、 B、 C、 D、2. 复数 (其中 为虚数单位), 为 的共轭复数,则 的虚部是( )A、 B、 C、 D、3. 已知实数 , 满足 ,则 的最小值是( )A、6 B、4 C、2 D、04. 下列说法正确的是( )A、命题“若 ,则 .”的否命题是“若 ,则 .” B、 是函数 在定义域上单调递增的充分不必要条件 C、 D、若命题 ,则5. 已知 ,则 ( )A、 B、 C、 D、6. 函数 的图象可能是( )A、
 B、
B、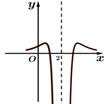 C、
C、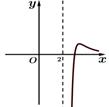 D、
D、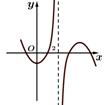 7. 若将函数 的图象向左平移 ( )个单位,所得图象关于原点对称,则 最小时, ( )A、 B、 C、 D、8. 现行普通高中生在高一升高二时面临着选文理的问题,某校抽取了部分男、女生意愿的一份样本,制作出如下两个等高条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
7. 若将函数 的图象向左平移 ( )个单位,所得图象关于原点对称,则 最小时, ( )A、 B、 C、 D、8. 现行普通高中生在高一升高二时面临着选文理的问题,某校抽取了部分男、女生意愿的一份样本,制作出如下两个等高条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( ) A、样本中的女生数量多于男生数量 B、样本中有理意愿的生数量多于有文意愿的生数量 C、样本中的男生偏爱理 D、样本中的女生偏爱文9. 某空间几何体的三视图如图所示,则该几何体的体积为( )
A、样本中的女生数量多于男生数量 B、样本中有理意愿的生数量多于有文意愿的生数量 C、样本中的男生偏爱理 D、样本中的女生偏爱文9. 某空间几何体的三视图如图所示,则该几何体的体积为( ) A、1 B、2 C、4 D、810. 在 中, 为斜边 边的高,若 , , ,则 ( )A、 B、 C、 D、11. 已知双曲线 : ( , )的一条渐近线为 ,圆 : 与 交于 , 两点,若 是等腰直角三角形,且 (其中 为坐标原点),则双曲线 的离心率为( )A、 B、 C、 D、12. 若函数 在 单调递增,则 的取值范围是( )A、 B、 C、 D、
A、1 B、2 C、4 D、810. 在 中, 为斜边 边的高,若 , , ,则 ( )A、 B、 C、 D、11. 已知双曲线 : ( , )的一条渐近线为 ,圆 : 与 交于 , 两点,若 是等腰直角三角形,且 (其中 为坐标原点),则双曲线 的离心率为( )A、 B、 C、 D、12. 若函数 在 单调递增,则 的取值范围是( )A、 B、 C、 D、二、填空题(每题5分,满分20分)
-
13. 展开式中的常数项为 ,则 .14. 若直线 与曲线 相切,则 .15. 有3女2男共5名志愿者要全部分到3个社区去参加志愿服务,每个社区1到2人,甲、乙两名女志愿者需到同一社区,男志愿者到不同社区,则不同的分法种数为 .16. 已知点 ,抛物线 : ( )的准线为 ,点 在 上,作 于 ,且 , ,则 .
三、解答题 (本大题共6小题,共70分.)
-
17. 设 为等差数列 的前n项和,已知 , .(1)、求 的通项公式;(2)、令 , ,若 对一切 成立,求实数m的最小值.18. 如图,在底面为菱形的四棱锥P-ABCD中, ,点E在PD上,且 .

(Ⅰ)求证: 平面ABCD;
(Ⅱ)求二面角E-AC-D的正弦值;
(Ⅲ)在棱PC上是否存在点F使得 平面EAC?若存在,试求PF的值;若不存在,请说明理由.
19. 某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为 、 、 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).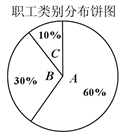

(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以( Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
20. 已知椭圆 ( )的两个焦点与短轴的一个端点是有一个角为 的等腰三角形的三个顶点,直线 : 与椭圆 有且只有一个公共点 .(Ⅰ)求椭圆 的方程及点 的坐标;
(Ⅱ)斜率为 的直线 与椭圆 交于不同的两点 、 ,且与直线 交于点 ,证明:存在常数 ,使得 成立,并求 的值.
21. 定义在R上的函数f (x)满足 .(Ⅰ)求函数f (x)的解析式;
(Ⅱ)求函数g (x)的单调区间;
(Ⅲ)如果s、t、r满足 ,那么称s比t更靠近r . 当a≥2且x≥1时,试比较 和 哪个更靠近lnx , 并说明理由.