2016-2017学年浙江省宁波市九校八年级下学期期中联考数学试卷

试卷更新日期：2017-05-23 类型：期中考试

进入出卷网下载

一、选择题

1. 若式子 $\frac{\sqrt{x+ 2}}{x- 1}$ 有意义，则x的取值范围是（）

A、x≥－2且x≠1 B、x＞－2且x≠1 C、x≥－2 D、x＞－2

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的有（）

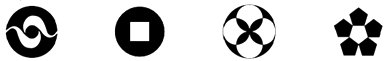A、4个 B、3个 C、2个 D、1个

查看试题解析
3.
某篮球队12名队员的年龄如下表所示，则这12名队员年龄的众数和平均数是（）

A、19，19.5 B、19，19 C、18，19.5 D、18，19

查看试题解析
4. 若关于x的一元二次方程(k+2)x²+3x+k²－k－6＝0必有一根为0，则k的值是（）

A、3 或－2 B、－3或2 C、3 D、－2

查看试题解析
5.
如图，小红在作线段AB的垂直平分线时，是这样操作的：分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧，相交于点C，D，则直线CD即为所求。连结AC，BC，AD，BD，根据她的作图方法可知，四边形ADBC一定是（）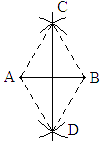

A、矩形 B、菱形 C、正方形 D、等腰梯形

查看试题解析
6.
如图，矩形ABCD的两条对角线相交于点O，∠AOB＝120°，AD＝2，点E是BC的中点，连结OE，则OE的长是（）

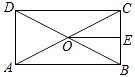A、 $\sqrt{3}$ B、2 $\sqrt{3}$ C、2 D、4

查看试题解析
7. 用反证法证明“在直角三角形中，至少有一个锐角不大于45º”，应先假设这个直角三角形中（）

A、有一个锐角小于45º B、每一个锐角都小于45º C、有一个锐角大于45º D、每一个锐角都大于45º

查看试题解析
8. 关于x的一元二次方程 $x^{2} - a x - 1 = 0$ （其中a为常数）的根的情况是（）

A、有两个不相等的实数根 B、可能有实数根，也可能没有实数根 C、有两个相等的实数根 D、没有实数根

查看试题解析
9. 如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（）

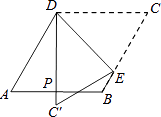A、78° B、75° C、60° D、45°

查看试题解析
10.
如图，△ACE是以▱ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称.若E点的坐标是（7，－3 $\sqrt{3}$ ），则D点的坐标是（）

A、(4，0) B、( $\frac{9}{2}$ ，0) C、(5，0) D、( $\frac{11}{2}$ ，0)

查看试题解析
11.
如图，①②③④⑤五个平行四边形拼成一个含30度内角的菱形EFGH（不重叠无缝隙）．若①②③④四个平行四边形面积的和为26cm² ，四边形ABCD面积是19cm² ，则①②③④四个平行四边形周长的总和为（）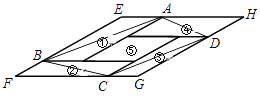

A、96cm B、64cm C、48cm D、36cm

查看试题解析
12. 我们规定：将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”，等积线被这个平面图形截得的线段叫做该图形的“等积线段”（例如三角形的中线就是三角形的等积线段）．已知菱形的边长为4，且有一个内角为60°，设它的等积线段长为m，则m的取值范围是.

查看试题解析
13. 下列属于一元二次方程的是（）

A、 $2 x = \frac{1}{5} x^{2}$ B、 $\frac{1}{x^{2}} + 2 x = 1$ C、 $3 y^{2} + 2 x - 5 = 0$ D、 $2 x - 1 = 0$

查看试题解析

二、填空题

14. 当x=－1时，二次根式 $\sqrt{3 -x}$ 的值是.

查看试题解析
15. 若一个多边形的内角和为720度，则这个多边形的边数是．

查看试题解析
16.
已知一组数据1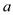，，3，2，4，它的平均数是3，这组数据的方差是.

查看试题解析
17. 如图，已知Rt△ABC中，∠ACB＝90°，以斜边AB为边向外作正方形ABDE，且正方形的对角线交于点O，连结OC．已知AC＝5，OC＝6 $\sqrt{2}$ ，则另一直角边BC的长为．

查看试题解析
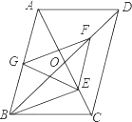
18.
平行四边形ABCD中，对角线AC、BD相交于点O，BD=2AD，E、F、G分别是OC、OD，AB的中点．下列结论：①EG=EF； ②△EFG≌△GBE； ③FB平分∠EFG；④EA平分∠GEF；⑤四边形BEFG是菱形．
其中正确的是.

查看试题解析

三、解答题

19. 计算：
（Ⅰ）( $\sqrt{48}$ － $\sqrt{27}$ )÷ $\sqrt{3}$
（Ⅱ） $\sqrt{（ 2 - \sqrt{5} ）^{2}} +| \sqrt{5} -3|$

查看试题解析
20. 解方程:
（Ⅰ） $x^{2} - 6 x= 1$ （Ⅱ） $（ x+ 4 ）^{2} = 5 （ x+ 4 ）$

查看试题解析
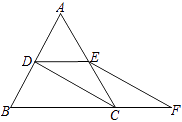
21.
如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF＝ $\frac{1}{2}$ BC，连结CD和EF.
（Ⅰ）求证：四边形CDEF是平行四边形；
（Ⅱ）求四边形BDEF的周长.

查看试题解析
22.
一家面临倒闭的企业在“调整产业结构，转变经营机制”的改革后，扭亏为盈. 下表是该企业2015年8～12月、2016年第一季度的月利润统计表：
根据以上信息，解答下列问题：

(1)、2015年8月至2016年1月该企业利润的月平均利润为万元，月利润的中位数为万元；

(2)、已知该企业2016年2、3月份的月利润的平均增长率相同，求这个平均增长率和2月份的月利润.

查看试题解析
23.
在边长为1的小正方形组成的方格纸中，若多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形．记格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为 $S = m a + n b - 1$ ，其中m，n为常数．
（Ⅰ）在下面的方格中各画出一个面积为6的格点多边形，依次为三角形、平行四边形（非菱形）、菱形；
（Ⅱ）利用（Ⅰ）中的格点多边形确定m，n的值．

查看试题解析
24. 水果批发市场有一种高档水果，如果每千克盈利（毛利润）10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销量将减少20千克．
（Ⅰ）若以每千克能盈利18元的单价出售，问每天的总毛利润为多少元?
（Ⅱ）现市场要保证每天总毛利润6000元，同时又要使顾客得到实惠，则每千克应涨价多少元?
（Ⅲ）现需按毛利润的10%交纳各种税费，人工费每日按销售量每千克支出0.9元，水电房租费每日102元，若剩下的每天总纯利润要达到5100元，则每千克涨价应为多少?

查看试题解析
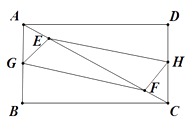
25.
四边形ABCD 中，AB=3，BC=4，E，F 是对角线 AC上的两个动点，分别从 A，C 同时出发，相向而行，速度均为 1cm/s，运动时间为 t 秒，当其中一个动点到达后就停止运动．
（Ⅰ）若 G，H 分别是 AB，DC 中点，求证：四边形 EGFH 始终是平行四边形．
（Ⅱ）在（1）条件下，当 t 为何值时，四边形 EGFH 为矩形．
（Ⅲ）若 G，H 分别是折线 A﹣B﹣C，C﹣D﹣A 上的动点，与 E，F 相同的速度同时出发，当 t 为何值时，四边形 EGFH 为菱形．

查看试题解析