广西八市2019年高考理数4月联合调研考试试卷
试卷更新日期:2019-05-28 类型:高考模拟
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知集合A={x|x2-x-6≥0},集合B={0,1,2,3,4},则A∩B=( )A、{4} B、{3,4} C、{2,3,4} D、{0,1,2,3,4}2. 若复数2满足(1+z)(1+i)=1+2i(i是虚数单位),则|z|=( )A、 B、 C、 D、3. 若向量a=(2,3),b=(x,2),且a·(a-2b)=3,则实数x的值为( )A、- B、 C、-3 D、34. 去年年底甲、乙、丙、丁四个县人口总数为m万,各县人口占比如图,其中丙县人口为70万,则去年年底甲县的人口为( )
 A、162万 B、176万 C、182万 D、186万5. 已知双曲线C: =1(a>0)的一个焦点为(2.0),则双曲线C的渐近线方程为( )A、y=±x B、y=± x C、y=± x D、y=±2x6. 已知数列(an)满足:a1=1,an+1=3an-2,则a6=( )A、0 B、1 C、2 D、67. 已知将函数f(x)=sin(2x+ )(0< <受)的围象向左平移 个单位长度后,得到函数g(x)的图象。若g(x)是偶函数,则f( )=( )A、 B、 C、 D、18. 已知x,y满足条件 ,若z=x+2y的最小值为0,则m=( )A、1 B、2 C、3 D、49. 曲线y= 与直线y=5-x围成的平面图形的面积为( )A、 B、 C、 -4ln2 D、 -8ln210. 已知抛物线x2=2py(p>0)的准线方程为y=-1,△ABC的顶点A在抛物线上,B,C两点在直线y=2x-5上,若 ,则△ABC面积的最小值为( )A、5 B、4 C、 D、111. 设过点P(-2,0)的直线l与圆C:x2+y2-4x-2y+1=0的两个交点为A,B,若 ,则lABl=( )A、 B、 C、 D、12. 已知一个四棱锥的三视图如图,图中网格小正方形边长为1,则该几何体的各条棱中,最长的棱的长度为( )
A、162万 B、176万 C、182万 D、186万5. 已知双曲线C: =1(a>0)的一个焦点为(2.0),则双曲线C的渐近线方程为( )A、y=±x B、y=± x C、y=± x D、y=±2x6. 已知数列(an)满足:a1=1,an+1=3an-2,则a6=( )A、0 B、1 C、2 D、67. 已知将函数f(x)=sin(2x+ )(0< <受)的围象向左平移 个单位长度后,得到函数g(x)的图象。若g(x)是偶函数,则f( )=( )A、 B、 C、 D、18. 已知x,y满足条件 ,若z=x+2y的最小值为0,则m=( )A、1 B、2 C、3 D、49. 曲线y= 与直线y=5-x围成的平面图形的面积为( )A、 B、 C、 -4ln2 D、 -8ln210. 已知抛物线x2=2py(p>0)的准线方程为y=-1,△ABC的顶点A在抛物线上,B,C两点在直线y=2x-5上,若 ,则△ABC面积的最小值为( )A、5 B、4 C、 D、111. 设过点P(-2,0)的直线l与圆C:x2+y2-4x-2y+1=0的两个交点为A,B,若 ,则lABl=( )A、 B、 C、 D、12. 已知一个四棱锥的三视图如图,图中网格小正方形边长为1,则该几何体的各条棱中,最长的棱的长度为( )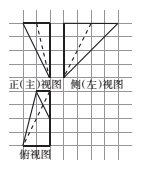 A、4 B、6 C、4 D、4
A、4 B、6 C、4 D、4二、填空题:本题共4小题,每小题5分,共20分
-
13. 二项式 的展开式中x4的系数为(用数字作答)14. 已知等差数列{an}的前n项和为Sn , 若a5=7,则S9= .15. 在直三棱柱ABC-A1B1C1中,AC=3,BC=3,AB=3 ,AA1=4,则异面直线A1C与BC1所成角的余弦值为 .16. 已知函数f(x)= ,当x∈(-∞,m]时,f(x)的取值范围为(-∞,1- ],则实数m的取值范围是 .
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤,第17~21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答。
-
17. 已知在△ABC中,A,B,C所对的边分别为a,b,c,若a2+b2-c2=8,△ABC的面积为2(1)、求角C的大小;(2)、若c=2 ,求sin A+sin B的值。18. 一汽车销售公司对开业4年来某种型号的汽车“五一”优惠金额与销售量之间的关系进分析研究并做了记录,得到如下资料。
日期
第1年
第2年
第3年
第4年
优惠金额x(千元)
10
11
13
12
销售量y(辆)
22
24
31
27
利用散点图可知x,y线性相关。
参考公式: ;
(1)、求出y关于x的线性回归方程 ;(2)、若第5年优惠金额8.5千元,估计第5年的销售量y(辆)的值.19. 如图,在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC⊥BC,AC=1,BC=2,AA1=4,M为侧面AA1C1C的对角线的交点,D、E分别为棱AB、BC的中点。 (1)、求证:平面MDE∥平面A1BC1;(2)、求二面角C-ME-D的余弦值。20. 已知曲线C上动点M与定点F(- ,0)的距离和它到定直线l1:x=-2的距离的比是常数 ,若过P(0,1)的动直线l与曲线C相交于A,B同点。(1)、说明曲线C的形状,并写出其标准方程;(2)、是否存在与点P不同的定点Q,使得 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由。21. 已知函数f(x)=ax2-2xln x-1(a∈R).(1)、若x= 时,函数f(x)取得极值,求函数f(x)的单调区间:(2)、证明:1+ + +…+ > 1n(2m+1)+ (n∈N*).
(1)、求证:平面MDE∥平面A1BC1;(2)、求二面角C-ME-D的余弦值。20. 已知曲线C上动点M与定点F(- ,0)的距离和它到定直线l1:x=-2的距离的比是常数 ,若过P(0,1)的动直线l与曲线C相交于A,B同点。(1)、说明曲线C的形状,并写出其标准方程;(2)、是否存在与点P不同的定点Q,使得 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由。21. 已知函数f(x)=ax2-2xln x-1(a∈R).(1)、若x= 时,函数f(x)取得极值,求函数f(x)的单调区间:(2)、证明:1+ + +…+ > 1n(2m+1)+ (n∈N*).