上海市黄浦区2019年中考数学二模试卷

试卷更新日期：2019-05-27 类型：中考模拟

进入出卷网下载

一、选择题（满分24分）

1. 下列自然数中，素数是（）

A、1 B、2 C、4 D、9

查看试题解析
2. 下列运算正确的是（）

A、（a²）³ B、 $a^{2} \cdot a^{3} = a^{5}$ C、 D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
3. 反比例函数 $y = \frac{m}{x}$ 的图像在第二、四象限内，则点 $(m, - 1)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 为了了解某校九年级400名学生的体重情况，从中抽取50名学生的体重进行分析.在这项调查中，样本是指（）

A、400名学生 B、被抽取的50名学生 C、400名学生的体重 D、被抽取的50名学生的体重

查看试题解析
5. 下列等式成立的是（）

A、 $- (- \vec{a}) = \vec{a}$ B、 $\vec{a} + (- \vec{a}) = 0$ C、 $\vec{a} - \vec{b} = \vec{b} - \vec{a}$ D、 $\vec{0} - \vec{a} = \vec{a}$

查看试题解析
6. 半径分别为1和5的两个圆相交，它们的圆心距可以是（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题：（满分48分）

7. 化简： $\sqrt{4}$ = ．

查看试题解析
8. 因式分解： $a^{2} - 9 =$ ．

查看试题解析
9. 方程 $\sqrt{x + 1} = 3$ 的解是 $x =$ ．

查看试题解析
10. 直线 $y = 2 x - 3$ 的截距是.

查看试题解析
11. 不等式组 ${\begin{cases} 2 x > 5, \\ x - 3 < 0 \end{cases}$ 的解集是.

查看试题解析
12. 如果关于x的方程 $x^{2} - (2 m - 1) x + m^{2} = 0$ 没有实数根，那么 $m$ 的取值范围是．

查看试题解析
13. 掷一枚质地均匀的正方体骰子，骰子的六个面分别标有1到6的点数，向上的一面出现的点数是2的倍数的概率是．

查看试题解析

14. 秋季新学期开学时，某中学对六年级新生掌握“中学生日常行为规范”的情况进行了知识测试，测试成绩全部合格，现学校随机选取了部分学生的成绩，整理并制作成了不完整的图表（如表所示），图表中c= ．

分数段	频数	频率
60≤x＜70	6	a
70≤x＜80	20	0.4
80≤x＜90	15	b
90≤x≤100	c	0.18

查看试题解析

15. 正九边形的中心角等于°．

查看试题解析
16. 如图，点O是 $Δ A B C$ 的重心，过点O作 $D E$ ∥ $A B$ ，分别交 $A C$ 、 $B C$ 于点 $D$ 、 $E$ ，如果 $\vec{A B} = \vec{a}$ ，那么 $\vec{D O} =$ (结果用 $\vec{a}$ 表示)．

查看试题解析
17. 如图，函数 $y = \frac{12}{x} (x > 0)$ 的图像经过△OAB的顶点B和边AB的中点C，如果点B的横坐标为3，则点C的坐标为．

查看试题解析
18. 如图，在 $Δ A B C$ 中， $∠ A C B = 90 °$ ， $\sin B = \frac{3}{5}$ ，将 $Δ A B C$ 绕顶点C顺时针旋转，得到 $Δ A_{1} B_{1} C$ ，点A、B分别与点 $A_{1}$ 、 $B_{1}$ 对应，边 $A_{1} B_{1}$ 分别交边AB、 $B C$ 于点D、E，如果点E是边 $A_{1} B_{1}$ 的中点，那么 $\frac{B D}{B_{1} C} =$ ．

查看试题解析

三、解答题：（满分78分）

19. 计算： $\frac{\sqrt{3}}{\tan 60 ° - \cos 30 °} - {(27)}^{\frac{1}{3}} + | 1 - \sqrt{3} | - {(\sqrt{2019})}^{0}$ .

查看试题解析
20. 解方程： $\frac{x + 2}{x - 2} - \frac{16}{x^{2} - 4} = \frac{1}{x + 2}$ ．

查看试题解析
21. 如图，已知 $⊙ O$ 是 $Δ A B C$ 的外接圆，圆心O在 $Δ A B C$ 的外部， $A B = A C = 4$ ， $B C = 4 \sqrt{3}$ ，求 $⊙ O$ 的半径.

查看试题解析
22. A、B两地相距30千米，已知甲、乙两人分别骑自行车和摩托车从A地出发前往B地，途中乙因修车耽误了些时间，然后又继续赶路.图中的线段OM和折线OCDE分别反映了甲、乙两人所行的路程y（千米）与时间x（分）的函数关系，根据图像提供的信息回答下列问题：

(1)、甲骑自行车的速度是千米/分钟；

(2)、两人第二次相遇时距离A地千米；

(3)、线段DE反映了乙修好车后所行的路程y（千米）与时间x（分）的函数关系.请求出线段DE的表达式及其定义域.

查看试题解析
23. 如图，已知四边形ABCD，AD∥BC，对角线AC、BD交于点O，DO=BO，过点C作CE⊥AC，交BD的延长线于点E，交AD的延长线于点F，且满足 $∠ D C E = ∠ A C B$ .

(1)、求证：四边形ABCD是矩形；

(2)、求证： $\frac{D E}{E F} = \frac{A D}{C D}$ .

查看试题解析
24. 如图，已知抛物线 $y = a x^{2} + b x + c$ 经过原点 $O (0 ， 0)$ 、 $A (2 ， 0)$ ，直线 $y = 2 x$ 经过抛物线的顶点 $B$ ，点 $C$ 是抛物线上一点，且位于对称轴的右侧，联结 $B C$ 、 $O C$ 、AB，过点 $C$ 作 $C E$ ∥ $x$ 轴，分别交线段 $O B$ 、 $A B$ 于点 $E$ 、 $F$ .

(1)、求抛物线的表达式；

(2)、当 $B C = C E$ 时，求证： $Δ B C E$ ∽ $Δ A B O$ ；

(3)、当 $∠ C B A = ∠ B O C$ 时，求点 $C$ 的坐标.

查看试题解析
25. 已知四边形ABCD中，AD∥BC， $∠ A B C = 2 ∠ C$ ，点E是射线AD上一点，点F是射线DC上一点，且满足 $∠ B E F = ∠ A$ .

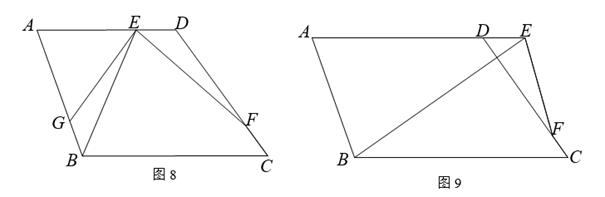(1)、如图8，当点E在线段AD上时，若AB=AD，在线段AB上截取AG=AE，联结GE.
求证：GE=DF；

(2)、如图9，当点E在线段AD的延长线上时，若AB=3，AD=4， $\cos A = \frac{1}{3}$ ，设 $A E = x$ ， $D F = y$ ，求 $y$ 关于 $x$ 的函数关系式及其定义域；

(3)、记BE与CD交于点M，在（2）的条件下，若△EMF与△ABE相似，求线段AE的长.

查看试题解析