江苏省无锡市华士片2017届九年级5月中考模拟数学试题
试卷更新日期:2017-05-22 类型:中考模拟
一、选择题
-
1. -3的倒数是( )
A、- B、 C、±3 D、32. 函数y= 中自变量x的取值范围是( )A、x>2 B、x≤2 C、x≥2 D、x≠23. 五多边形的内角和为 ( )A、180° B、360° C、540° D、720°4. 下列汽车标志中,是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 5.
5.如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于 ( )
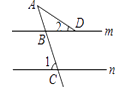 A、30° B、35° C、40° D、50°6. 若一组数据2、4、6、8、x的方差比另一组数据5、7、9、11、13的方差大,则 x 的值可以为( )
A、30° B、35° C、40° D、50°6. 若一组数据2、4、6、8、x的方差比另一组数据5、7、9、11、13的方差大,则 x 的值可以为( )
A、12 B、10 C、2 D、07. 已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
A、2 B、4 C、6 D、88. 过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其正确展开图为( )A、 B、
B、 C、
C、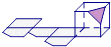 D、
D、 9. 对于代数式x2-10x+24,下列说法:①它是二次三项式; ②该代数式的值可能等于2017;③分解因式的结果是(x-4)(x-6);④该代数式的值可能小于-1.其中正确的有( )
9. 对于代数式x2-10x+24,下列说法:①它是二次三项式; ②该代数式的值可能等于2017;③分解因式的结果是(x-4)(x-6);④该代数式的值可能小于-1.其中正确的有( )
A、1个 B、2个 C、3 个 D、4个10. 在△ABC中,∠B=45°,AC=4,则△ABC面积的最大值为 ( )
A、4 B、4 +4 C、8 D、8 +8二、填空题.
-
11. 4的平方根为 .
12. 人体中红细胞的直径约为0.000 0077m,用科学记数法表示这个数为 m.
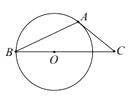
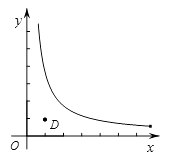
13. 计算: = .14. 若点A(-1,a)在反比例函数y=- 的图像上,则a的值为 .15.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心O.若∠B=25°,
则∠C=°.
 16.
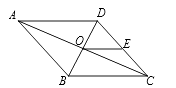
16.如图,菱形ABCD中,对角线AC交BD于O, E是CD的中点,且OE=2,则菱形
ABCD的周长等于 .
 17. 一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需的最少费用是 .
17. 一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需的最少费用是 .型号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
18. 在△ABC中,AB=4 ,BC=6,∠B=45°,D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,则CD的取值范围是 .
三、解答题
-
19. 计算:(1)、
(2)、(x-1)2-(x+1)(x-3).20. 计算:
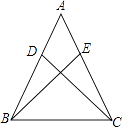
(1)、解方程: ;(2)、解不等式组:21.如图,△ABC中,AB=AC,点D、E分别在AB、AC边上,且∠EBC=∠DCB.
求证:BE=CD
 22.
22.在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下两幅统计图.请根据相关信息,解答下列问题:
 (1)、扇形统计图中,初赛成绩为1.65m所在扇形图形的圆心角为°;(2)、补全条形统计图;(3)、这组初赛成绩的中位数是m;(4)、根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.60m的运动员杨强能否进入复赛?为什么?23. 若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若一个三位数的十位上数字为7,且从4、5、6、8中随机选取两数,与7组成“中高数”,那么组成“中高数”的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)24.
(1)、扇形统计图中,初赛成绩为1.65m所在扇形图形的圆心角为°;(2)、补全条形统计图;(3)、这组初赛成绩的中位数是m;(4)、根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.60m的运动员杨强能否进入复赛?为什么?23. 若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若一个三位数的十位上数字为7,且从4、5、6、8中随机选取两数,与7组成“中高数”,那么组成“中高数”的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)24.如图,菱形ABCD中,
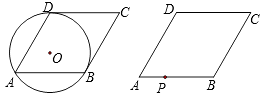 (1)、若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;(2)、若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)
(1)、若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;(2)、若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)
25. “夕阳红”养老院共有普通床位和高档床位共500张.已知今年一月份入住普通床位老人300人,入住高档床位老人90人,共计收费51万元;今年二月份入住普通床位老人350人,入住高档床位老人100人,共计收费58万元.(1)、求普通床位和高档床位每月收费各多少元?(2)、根据国家养老政策规定,为保障普通居民的养老权益,所有实际入住高档床位数不得超过普通床位数的三分之一;另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴.经测算,该养老院普通床位的运营成本是每月1200元/张,入住率为90%;高档床位的运营成本是每月2000元/张,入住率为70%.问该养老院应该怎样安排500张床的普通床位和高档床位数量,才能使每月的利润最大,最大为多少元?(月利润=月收费-月成本+月补贴)26.如图,已知抛物线 (其中 )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
 (1)、求抛物线的关系式;(2)、过点 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
(1)、求抛物线的关系式;(2)、过点 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
27.如图,在平面直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC.点E是y轴上任意一点记点E为(0,n).
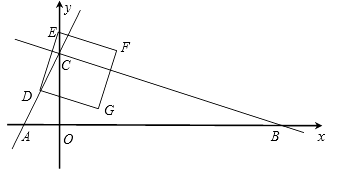 (1)、求直线BC的关系式;(2)、连结DE,将线段DE绕点D按顺时针旋转90°得线段DG,作正方形DEFG,是否存在n的值,使正方形DEFG的顶点F落在△ABC的边上?若存在,求出所有的n值并直接写出此时正方形DEFG与△ABC重叠部分的面积;若不存在,请说明理由.
(1)、求直线BC的关系式;(2)、连结DE,将线段DE绕点D按顺时针旋转90°得线段DG,作正方形DEFG,是否存在n的值,使正方形DEFG的顶点F落在△ABC的边上?若存在,求出所有的n值并直接写出此时正方形DEFG与△ABC重叠部分的面积;若不存在,请说明理由.
28.在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1 , A2B2C2D2 , AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.
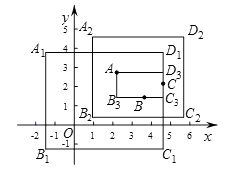
 (1)、已知A( 2,3),B(5,0),C( , 2).
(1)、已知A( 2,3),B(5,0),C( , 2).①当 时,点A,B,C的最优覆盖矩形的面积为;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为;
(2)、已知点D(1,1),点E( , ),其中点E是函数 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.