2014年江苏省南京市中考数学试卷
试卷更新日期:2017-05-22 类型:中考真卷
一、选择题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、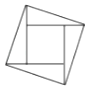 C、
C、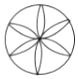 D、
D、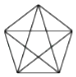 2. 计算(﹣a2)3的结果是( )A、a5 B、﹣a5 C、a6 D、﹣a63. 若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )A、1:2 B、2:1 C、1:4 D、4:14. 下列无理数中,在﹣2与1之间的是( )A、﹣ B、﹣ C、 D、5. 8的平方根是( )A、4 B、±4 C、2 D、6. 如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
2. 计算(﹣a2)3的结果是( )A、a5 B、﹣a5 C、a6 D、﹣a63. 若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为( )A、1:2 B、2:1 C、1:4 D、4:14. 下列无理数中,在﹣2与1之间的是( )A、﹣ B、﹣ C、 D、5. 8的平方根是( )A、4 B、±4 C、2 D、6. 如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )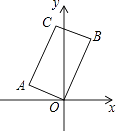 A、( ,3)、(﹣ ,4) B、( ,3)、(﹣ ,4) C、( , )、(﹣ ,4) D、( , )、(﹣ ,4)
A、( ,3)、(﹣ ,4) B、( ,3)、(﹣ ,4) C、( , )、(﹣ ,4) D、( , )、(﹣ ,4)二、填空题
-
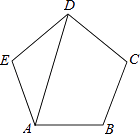
7. ﹣2的相反数是 , ﹣2的绝对值是 .8. 截止2013年底,中国高速铁路营运里程达到11000km,居世界首位,将11000用科学记数法表示为 .9. 使式子1+ 有意义的x的取值范围是 .10. 2014年南京青奥会某项目6名礼仪小姐的身高如下(单位:cm):168,166,168,167,169,168,则她们身高的众数是cm,极差是cm.11. 已知反比例函数y= 的图象经过点A(﹣2,3),则当x=﹣3时,y= .12. 如图,AD是正五边形ABCDE的一条对角线,则∠BAD= .
 13. 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2 cm,∠BCD=22°30′,则⊙O的半径为cm.
13. 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2 cm,∠BCD=22°30′,则⊙O的半径为cm. 14. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为cm.
14. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为cm. 15. 铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为cm.16. 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
15. 铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为cm.16. 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:x
…
﹣1
0
1
2
3
…
y
…
10
5
2
1
2
…
则当y<5时,x的取值范围是 .
三、解答题
-
17. 解不等式组: .18. 先化简,再求值: ﹣ ,其中a=1.19. 如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
 (1)、求证:四边形DBFE是平行四边形;(2)、当△ABC满足什么条件时,四边形DBFE是菱形?为什么?20. 从甲、乙、丙3名同学中随机抽取环保志愿者,求下列事件的概率;(1)、抽取1名,恰好是甲;(2)、抽取2名,甲在其中.21. 为了了解某市120000名初中学生的视力情况,某校数学兴趣小组收集有关数据,并进行整理分析.(1)、小明在眼镜店调查了1000名初中学生的视力,小刚在邻居中调查了20名初中学生的视力,他们的抽样是否合理?并说明理由.(2)、该校数学兴趣小组从该市七、八、九年级各随机抽取了1000名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.
(1)、求证:四边形DBFE是平行四边形;(2)、当△ABC满足什么条件时,四边形DBFE是菱形?为什么?20. 从甲、乙、丙3名同学中随机抽取环保志愿者,求下列事件的概率;(1)、抽取1名,恰好是甲;(2)、抽取2名,甲在其中.21. 为了了解某市120000名初中学生的视力情况,某校数学兴趣小组收集有关数据,并进行整理分析.(1)、小明在眼镜店调查了1000名初中学生的视力,小刚在邻居中调查了20名初中学生的视力,他们的抽样是否合理?并说明理由.(2)、该校数学兴趣小组从该市七、八、九年级各随机抽取了1000名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.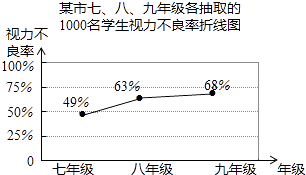
请你根据抽样调查的结果,估计该市120000名初中学生视力不良的人数是多少?
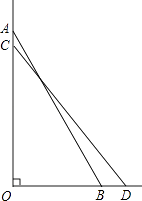
22. 某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年增长的百分率为x.(1)、用含x的代数式表示第3年的可变成本为万元;(2)、如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.23. 如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.(参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)
 24. 已知二次函数y=x2﹣2mx+m2+3(m是常数).(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?25. 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.
24. 已知二次函数y=x2﹣2mx+m2+3(m是常数).(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?25. 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.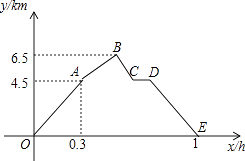 (1)、小明骑车在平路上的速度为km/h;他途中休息了h;(2)、求线段AB、BC所表示的y与x之间的函数关系式;(3)、如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?26. 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆.
(1)、小明骑车在平路上的速度为km/h;他途中休息了h;(2)、求线段AB、BC所表示的y与x之间的函数关系式;(3)、如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?26. 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆.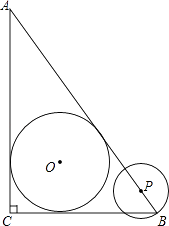 (1)、求⊙O的半径;(2)、点P从点B沿边BA向点A以1cm/s的速度匀速运动,以P为圆心,PB长为半径作圆,设点P运动的时间为t s,若⊙P与⊙O相切,求t的值.27. 【问题提出】
(1)、求⊙O的半径;(2)、点P从点B沿边BA向点A以1cm/s的速度匀速运动,以P为圆心,PB长为半径作圆,设点P运动的时间为t s,若⊙P与⊙O相切,求t的值.27. 【问题提出】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.

【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)、如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 , 可以知道Rt△ABC≌Rt△DEF.第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)、如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)、在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)(4)、∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若 , 则△ABC≌△DEF.