2014年江苏省连云港市中考数学试卷

试卷更新日期：2017-05-22 类型：中考真卷

进入出卷网下载

一、单项选择题

1. 下列实数中，是无理数的为（）

A、﹣1 B、﹣ $\frac{1}{2}$ C、 $\sqrt{2}$ D、3.14

查看试题解析
2. 计算 $\sqrt{{(- 3)}^{2}}$ 的结果是（）

A、﹣3 B、3 C、﹣9 D、9

查看试题解析
3. 在平面直角坐标系内，点P（﹣2，3）关于原点的对称点Q的坐标为（）

A、（2，﹣3） B、（2，3） C、（3，﹣2） D、（﹣2，﹣3）

查看试题解析
4. “丝绸之路”经济带首个实体平台﹣﹣中哈物流合作基地在我市投入使用，其年最大装卸能力达410000标箱．其中“410000”用科学记数法表示为（）

A、0.41×10⁶ B、4.1×10⁵ C、41×10⁴ D、4.1×10⁴

查看试题解析
5. 一组数据1，3，6，1，2的众数和中位数分别是（）

A、1，6 B、1，1 C、2，1 D、1，2

查看试题解析
6. 如图，若△ABC和△DEF的面积分别为S₁、S₂ ，则（）

A、S₁= $\frac{1}{2}$ S₂ B、S₁= $\frac{7}{2}$ S₂ C、S₁=S₂ D、S₁= $\frac{8}{5}$ S₂

查看试题解析
7. 如图，点P在以AB为直径的半圆内，连接AP、BP，并延长分别交半圆于点C、D，连接AD、BC并延长交于点F，作直线PF，下列说法一定正确的是（）
①AC垂直平分BF；②AC平分∠BAF；③FP⊥AB；④BD⊥AF．

A、①③ B、①④ C、②④ D、③④

查看试题解析
8. 如图，△ABC的三个顶点分别为A（1，2），B（2，5），C（6，1）．若函数y= $\frac{k}{x}$ 在第一象限内的图象与△ABC有交点，则k的取值范围是（）

A、2≤k≤ $\frac{49}{4}$ B、6≤k≤10 C、2≤k≤6 D、2≤k≤ $\frac{25}{2}$

查看试题解析

二、填空题

9. 使 $\sqrt{x - 1}$ 有意义的x的取值范围是．

查看试题解析
10. 计算：（2x+1）（x﹣3）= ．

查看试题解析
11. 一个正多边形的一个外角等于30°，则这个正多边形的边数为．

查看试题解析
12. 若ab=3，a﹣2b=5，则a²b﹣2ab²的值是．

查看试题解析
13. 若函数y= $\frac{m - 1}{x}$ 的图象在同一象限内，y随x增大而增大，则m的值可以是（写出一个即可）．

查看试题解析
14. 如图，AB∥CD，∠1=62°，FG平分∠EFD，则∠2= ．

查看试题解析
15. 如图1，折线段AOB将面积为S的⊙O分成两个扇形，大扇形、小扇形的面积分别为S₁、S₂ ，若 $\frac{S_{1}}{S} = \frac{S_{2}}{S_{1}}$ =0.618，则称分成的小扇形为“黄金扇形”．生活中的折扇（如图2）大致是“黄金扇形”，则“黄金扇形”的圆心角约为°．（精确到0.1）

查看试题解析
16. 如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF．如图2，展开后再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为点M，EM交AB于N，则tan∠ANE= ．

查看试题解析

三、解答题

17. 计算|﹣5|+ $\sqrt[3]{27}$ ﹣（ $\frac{1}{3}$ ）^﹣¹ ．

查看试题解析
18. 解不等式2（x﹣1）+5＜3x，并把解集在数轴上表示出来．

查看试题解析
19. 解方程： $\frac{2}{x - 2}$ +3= $\frac{1 - x}{2 - x}$ ．

查看试题解析
20. 我市启动了第二届“美丽港城，美在阅读”全民阅读活动，为了解市民每天的阅读时间情况，随机抽取了部分市民进行调查，根据调查结果绘制如下尚不完整的频数分布表：
阅读时间
x（min）
0≤x＜30
30≤x＜60
60≤x＜90
x≥90
合计
频数
450
400

50

频率

0.4
0.1

1

(1)、补全表格；

(2)、将每天阅读时间不低于60min的市民称为“阅读爱好者”，若我市约有500万人，请估计我市能称为“阅读爱好者”的市民约有多少万人？

查看试题解析
21. 如图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD．

(1)、求证：四边形OCED为菱形；

(2)、连接AE、BE，AE与BE相等吗？请说明理由．

查看试题解析
22. 如图1，在一个不透明的袋中装有四个球，分别标有字母A、B、C、D，这些球除了所标字母外都相同，另外，有一面白色、另一面黑色、大小相同的4张正方形卡片，每张卡片上面的字母相同，分别标有A、B、C、D．最初，摆成图2的样子，A、D是黑色，B、C是白色．
操作：①从袋中任意取一个球；
②将与取出球所标字母相同的卡片翻过来；
③将取出的球放回袋中
再次操作后，观察卡片的颜色．
（如：第一次取出球A，第二次取出球B，此时卡片的颜色变）

(1)、求四张卡片变成相同颜色的概率；

(2)、求四张卡片变成两黑两白，并恰好形成各自颜色矩形的概率．

查看试题解析
23. 小林在某商店购买商品A、B共三次，只有一次购买时，商品A、B同时打折，其余两次均按标价购买，三次购买商品A、B的数量和费用如下表：

购买商品A的数量（个）
购买商品B的数量（个）
购买总费用（元）
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062

(1)、小林以折扣价购买商品A、B是第次购物；

(2)、求出商品A、B的标价；

(3)、若商品A、B的折扣相同，问商店是打几折出售这两种商品的？

查看试题解析
24. 在一次科技活动中，小明进行了模拟雷达扫描实验．如图，表盘是△ABC，其中AB=AC，∠BAC=120°，在点A处有一束红外光线AP，从AB开始，绕点A逆时针匀速旋转，每秒钟旋转15°，到达AC后立即以相同旋转速度返回AB，到达后立即重复上述旋转过程．小明通过实验发现，光线从AB处旋转开始计时，旋转1秒，此时光线AP交BC边于点M，BM的长为（20 $\sqrt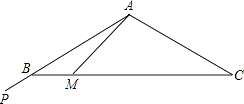{3}$ ﹣20）cm．

(1)、求AB的长；

(2)、从AB处旋转开始计时，若旋转6秒，此时光线AP与BC边的交点在什么位置？若旋转2014秒，交点又在什么位置？请说明理由．

查看试题解析
25. 为了考察冰川的融化状况，一支科考队在某冰川上设定一个以大本营O为圆心，半径为4km的圆形考察区域，线段P₁P₂是冰川的部分边界线（不考虑其它边界），当冰川融化时，边界线沿着与其垂直的方向朝考察区域平行移动，若经过n年，冰川的边界线P₁P₂移动的距离为s（km），并且s与n（n为正整数）的关系是s= $\frac{3}{20}$ n²﹣ $\frac{9}{50}$ n+ $\frac{7}{25}$ ．以O为原点，建立如图所示的平面直角坐标系，其中P₁、P₂的坐标分别为（﹣4，9）、（﹣13、﹣3）．

(1)、求线段P₁P₂所在直线对应的函数关系式；

(2)、求冰川边界线移动到考察区域所需的最短时间．

查看试题解析
26. 已知二次函数y=x²+bx+c，其图象抛物线交x轴于点A（1，0），B（3，0），交y轴于点C，直线l过点C，且交抛物线于另一点E（点E不与点A、B重合）．

(1)、求此二次函数关系式；

(2)、若直线l₁经过抛物线顶点D，交x轴于点F，且l₁∥l，则以点C、D、E、F为顶点的四边形能否为平行四边形？若能，求出点E的坐标；若不能，请说明理由．

(3)、
若过点A作AG⊥x轴，交直线l于点G，连接OG、BE，试证明OG∥BE．

查看试题解析
27.
某数学兴趣小组对线段上的动点问题进行探究，已知AB=8．
问题思考：
如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC、BPEF．

(1)、当点P运动时，这两个正方形的面积之和是定值吗？若是，请求出；若不是，请求出这两个正方形面积之和的最小值．

(2)、分别连接AD、DF、AF，AF交DP于点K，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由．
问题拓展：

(3)、
如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8．若点P从点A出发，沿A→B→C→D的线路，向点D运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长．

(4)、
如图3，在“问题思考”中，若点M、N是线段AB上的两点，且AM=BN=1，点G、H分别是边CD、EF的中点，请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+OB的最小值．

查看试题解析

	购买商品A的数量（个）	购买商品B的数量（个）	购买总费用（元）
第一次购物	6	5	1140
第二次购物	3	7	1110
第三次购物	9	8	1062