2013年江苏省镇江市中考数学试卷

试卷更新日期：2017-05-22 类型：中考真卷

进入出卷网下载

一、填空题

1. $\frac{1}{3}$ 的相反数是．

查看试题解析
2. 计算：（﹣2）× $\frac{1}{2}$ = ．

查看试题解析
3. 代数式 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
4. 化简：（x+1）²﹣2x= ．

查看试题解析
5. 若x³=8，则x= ．

查看试题解析
6. 如图，AD平分△ABC的外角∠EAC，且AD∥BC，若∠BAC=80°，则∠B=°．

查看试题解析
7. 有一组数据：2，3，5，5，x，它们的平均数是10，则这组数据的众数是．

查看试题解析
8. 写一个你喜欢的实数m的值，使关于x的一元二次方程x²﹣x+m=0有两个不相等的实数根．

查看试题解析
9. 已知点P（a，b）在一次函数y=4x+3的图象上，则代数式4a﹣b﹣2的值等于．

查看试题解析
10. 如图，AB是半圆O的直径，点P在AB的延长线上，PC切半圆O于点C，连接AC．若∠CPA=20°，则∠A=°．

查看试题解析
11. 地震中里氏震级增加1级，释放的能量增大到原来的32倍，那么里氏级地震释放的能量是3级地震释放能量的32⁴倍．

查看试题解析
12. 如图，五边形ABCDE中，AB⊥BC，AE∥CD，∠A=∠E=120°，AB=CD=1，AE=2，则五边形ABCDE的面积等于．

查看试题解析

二、选择题

13. 下列运算正确的是（）

A、x﹣2x=x B、（xy²）⁰=xy² C、 ${(- \sqrt{2})}^{2} = 4$ D、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$

查看试题解析
14. 二次函数y=x²﹣4x+5的最小值是（）

A、﹣1 B、1 C、3 D、5

查看试题解析
15. 用半径为6的半圆围成一个圆锥的侧面，则圆锥的底面半径等于（）

A、3 B、 $\frac{5}{2}$ C、2 D、 $\frac{3}{2}$

查看试题解析
16. 已知关于x的方程2x+4=m﹣x的解为负数，则m的取值范围是（）

A、 $m < \frac{4}{3}$ B、 $m > \frac{4}{3}$ C、m＜4 D、m＞4

查看试题解析
17.
如图，A、B、C是反比例函数y= $\frac{k}{x}$ （k＜0）图象上三点，作直线l，使A、B、C到直线l的距离之比为3：1：1，则满足条件的直线l共有（）

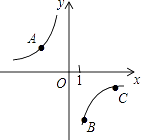A、4条 B、3条 C、2条 D、1条

查看试题解析

三、解答题

18.

(1)、计算： $2^{- 2} + | - \frac{1}{4} | - {(π - 2013)}^{0}$ ；

(2)、化简： $(\frac{1}{2} - \frac{a}{2 a + 2}) \div \frac{a}{a + 1}$ ．

查看试题解析
19.

(1)、解方程： $\frac{1}{x + 2} + \frac{1}{2 x - 1} = 0$

(2)、解不等式组： ${\begin{cases} 3 x - 2 \geq 1 \\ x + 9 < 3 (x + 1) \end{cases}$ ．

查看试题解析
20. 算式：1△1△1=□，在每一个“△”中添加运算符号“+”或“﹣”后，通过计算，“□”中可得到不同的运算结果．求运算结果为1的概率．

查看试题解析
21. 如图，AB∥CD，AB=CD，点E、F在BC上，且BE=CF．

(1)、求证：△ABE≌△DCF；

(2)、试证明：以A、F、D、E为顶点的四边形是平行四边形．

查看试题解析
22. 某市对一大型超市销售的甲、乙、丙3种大米进行质量检测．共抽查大米200袋，质量评定分为A、B两个等级（A级优于B级），相应数据的统计图如下：
根据所给信息，解决下列问题：

(1)、a= ， b=；

(2)、已知该超市现有乙种大米750袋，根据检测结果，请你估计该超市乙种大米中有多少袋B级大米？

(3)、对于该超市的甲种和丙种大米，你会选择购买哪一种？运用统计知识简述理由．

查看试题解析
23.
如图，小明在教学楼上的窗口A看地面上的B、C两个花坛，测得俯角∠EAB=30°，俯角∠EAC=45°．已知教学楼基点D与点C、B在同一条直线上，且B、C两花坛之间的距离为6m．求窗口A到地面的高度AD．（结果保留根号）

查看试题解析
24. 如图，抛物线y=ax²+bx（a＞0）经过原点O和点A（2，0）．

(1)、写出抛物线的对称轴与x轴的交点坐标；

(2)、点（x₁ ， y₁），（x₂ ， y₂）在抛物线上，若x₁＜x₂＜1，比较y₁ ， y₂的大小；

(3)、点B（﹣1，2）在该抛物线上，点C与点B关于抛物线的对称轴对称，求直线AC的函数关系式．

查看试题解析
25. 如图1，Rt△ABC中，∠ACB=90°，AB=5，BC=3，点D在边AB的延长线上，BD=3，过点D作DE⊥AB，与边AC的延长线相交于点E，以DE为直径作⊙O交AE于点F．

(1)、求⊙O的半径及圆心O到弦EF的距离；

(2)、连接CD，交⊙O于点G（如图2）．求证：点G是CD的中点．

查看试题解析
26. “绿色出行，低碳健身”已成为广大市民的共识．某旅游景点新增了一个公共自行车停车场，6：00至18：00市民可在此借用自行车，也可将在各停车场借用的自行车还于此地．林华同学统计了周六该停车场各时段的借、还自行车数，以及停车场整点时刻的自行车总数（称为存量）情况，表格中x=1时的y值表示7：00时的存量，x=2时的y值表示8：00时的存量…依此类推．他发现存量y（辆）与x（x为整数）满足如图所示的一个二次函数关系．
时段
x
还车数
（辆）
借车数
（辆）
存量y
（辆）
6：00﹣7：00
1
45
5
100
7：00﹣8：00
2
43
11
n
…
…
…
…
…
根据所给图表信息，解决下列问题：

(1)、m= ，解释m的实际意义：；

(2)、求整点时刻的自行车存量y与x之间满足的二次函数关系式；

(3)、已知9：00～10：O0这个时段的还车数比借车数的3倍少4，求此时段的借车数．

查看试题解析
27.
通过对苏科版八（下）教材一道习题的探索研究，我们知道：一次函数y=x﹣1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的，函数 $y = \frac{k}{x + 2} (k \neq 0)$ 的图象是由反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象向左平移2个单位长度得到．灵活运用这一知识解决问题．如图，已知反比例函数 $y = \frac{4}{x}$ 的图象C与正比例函数y=ax（a≠0）的图象l相交于点A（2，2）和点B．

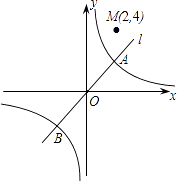(1)、写出点B的坐标，并求a的值；

(2)、将函数 $y = \frac{4}{x}$ 的图象和直线AB同时向右平移n（n＞0）个单位长度，得到的图象分别记为C′和l′，已知图象C′经过点M（2，4）．
①求n的值；
②分别写出平移后的两个图象C′和l′对应的函数关系式；
③直接写出不等式 $\frac{4}{x - 1} \leq a x - 1$ 的解集．

查看试题解析
28. 【阅读】
如图1，在平面直角坐标系xOy中，已知点A（a，0）（a＞0），B（2，3），C（0，3）．过原点O作直线l，使它经过第一、三象限，直线l与y轴的正半轴所成角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．

(1)、【理解】
若点D与点A重合，则这个操作过程为FZ[ ， ]；

(2)、【尝试】
若点D恰为AB的中点（如图2），求θ；

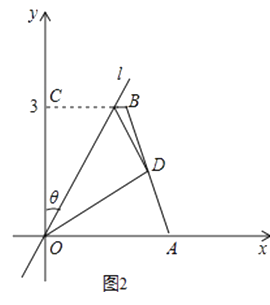(3)、经过FZ[45°，a]操作，点B落在点E处，若点E在四边形0ABC的边AB上，求出a的值；若点E落在四边形0ABC的外部，直接写出a的取值范围；

(4)、【探究】
经过FZ[θ，a]操作后，作直线CD交x轴于点G，交直线AB于点H，使得△ODG与△GAH是一对相似的等腰三角形，直接写出FZ[θ，a]．

查看试题解析

时段	x	还车数（辆）	借车数（辆）	存量y （辆）
6：00﹣7：00	1	45	5	100
7：00﹣8：00	2	43	11	n
…	…	…	…	…