2013年江苏省盐城市中考数学试卷
试卷更新日期:2017-05-22 类型:中考真卷
一、选择题
-
1. ﹣2、0、1、﹣3四个数中,最小的数是( )A、﹣2 B、0 C、1 D、﹣32. 如果收入50元,记作+50元,那么支出30元记作( )A、+30元 B、﹣30元 C、+80元 D、﹣80元3. 下面的几何体中,主视图不是矩形的是( )A、
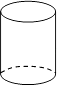 B、
B、 C、
C、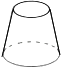 D、
D、 4. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≥3 B、x≤3 C、x>3 D、x<35. 下列运算中,正确的是( )A、2a2+3a2=a4 B、5a2﹣2a2=3 C、a3×2a2=2a6 D、3a6÷a2=3a46. 某公司10名职工5月份工资统计如下,该公司10名职工5月份工资的众数和中位数分别是( )
4. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≥3 B、x≤3 C、x>3 D、x<35. 下列运算中,正确的是( )A、2a2+3a2=a4 B、5a2﹣2a2=3 C、a3×2a2=2a6 D、3a6÷a2=3a46. 某公司10名职工5月份工资统计如下,该公司10名职工5月份工资的众数和中位数分别是( )工资(元)
2000
2200
2400
2600
人数(人)
1
3
4
2
A、2400元、2400元 B、2400元、2300元 C、2200元、2200元 D、2200元、2300元7. 如图,直线a∥b,∠1=120°,∠2=40°,则∠3等于( )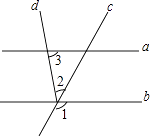 A、60° B、70° C、80° D、90°8. 如图①是3×3正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有( )
A、60° B、70° C、80° D、90°8. 如图①是3×3正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有( )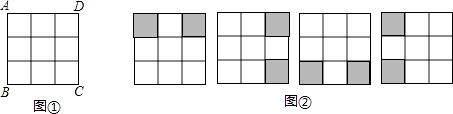 A、4种 B、5种 C、6种 D、7种
A、4种 B、5种 C、6种 D、7种二、填空题
-
9. 16的平方根是 .10. 因式分解:a2﹣9= .
11. 2013年4月20日,四川省雅安市芦山县发生7.0级地震.我市爱心人士情系灾区,积极捐款,截止到5月6日,市红十字会共收到捐款约1400000元,这个数据用科学记数法可表示为元.12. 使分式 的值为零的条件是x= .13. 如图所示是一飞镖游戏板,大圆的直径把一组同心圆分成四等份,假设飞镖击中圆面上每一个点都是等可能的,则飞镖落在黑色区域的概率是 . 14. 若x2﹣2x=3,则代数式2x2﹣4x+3的值为 .15. 写出一个过点(0,3),且函数值y随自变量x的增大而减小的一次函数关系式: . (填上一个答案即可)16. 如图,将⊙O沿弦AB折叠,使 经过圆心O,则∠OAB= .
14. 若x2﹣2x=3,则代数式2x2﹣4x+3的值为 .15. 写出一个过点(0,3),且函数值y随自变量x的增大而减小的一次函数关系式: . (填上一个答案即可)16. 如图,将⊙O沿弦AB折叠,使 经过圆心O,则∠OAB= .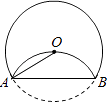 17. 如图,在△ABC中,∠BAC=90°,AB=5cm,AC=2cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中的阴影部分)的面积为cm2 .
17. 如图,在△ABC中,∠BAC=90°,AB=5cm,AC=2cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中的阴影部分)的面积为cm2 .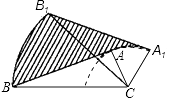 18. 如图,在以点O为原点的平面直角坐标系中,一次函数y=﹣ x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC= AB,反比例函数y= 的图象经过点C,则所有可能的k值为 .
18. 如图,在以点O为原点的平面直角坐标系中,一次函数y=﹣ x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC= AB,反比例函数y= 的图象经过点C,则所有可能的k值为 .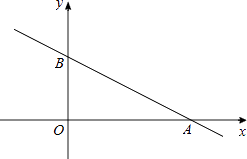
三、解答题
-
19.(1)、计算:2+|﹣3|+tan45°;(2)、解不等式:3(x﹣1)>2x+2.20. 先化简,再求值:(x﹣1)÷( ﹣1),其中x为方程x2+3x+2=0的根.21. 市交警支队对某校学生进行交通安全知识宣传,事先以无记名的方式随机调查了该校部分学生闯红灯的情况,并绘制成如图所示的统计图.请根据图中的信息回答下列问题:
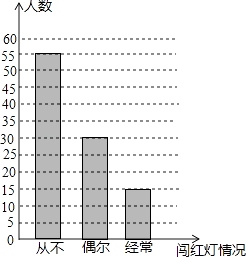 (1)、本次共调查了多少名学生?(2)、如果该校共有1500名学生,请你估计该校经常闯红灯的学生大约有多少人;(3)、针对图中反映的信息谈谈你的认识.(不超过30个字)22. 一只不透明的袋子,装有分别标有数字1、2、3的三个球,这些球除所标的数字外都相同,搅匀后从中摸出1个球,记录下数字后放回袋中并搅匀,再从中任意摸出1个球,记录下数字,请用列表或画树状图的方法,求出两次摸出的球上的数字之和为偶数的概率.23. 如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.
(1)、本次共调查了多少名学生?(2)、如果该校共有1500名学生,请你估计该校经常闯红灯的学生大约有多少人;(3)、针对图中反映的信息谈谈你的认识.(不超过30个字)22. 一只不透明的袋子,装有分别标有数字1、2、3的三个球,这些球除所标的数字外都相同,搅匀后从中摸出1个球,记录下数字后放回袋中并搅匀,再从中任意摸出1个球,记录下数字,请用列表或画树状图的方法,求出两次摸出的球上的数字之和为偶数的概率.23. 如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.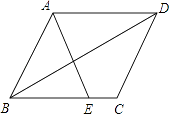 (1)、求证:∠ABE=∠EAD;(2)、若∠AEB=2∠ADB,求证:四边形ABCD是菱形.24. 实践操作
(1)、求证:∠ABE=∠EAD;(2)、若∠AEB=2∠ADB,求证:四边形ABCD是菱形.24. 实践操作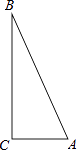
如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)、作∠BAC的平分线,交BC于点O;(2)、以O为圆心,OC为半径作圆.(3)、在你所作的图中,AB与⊙O的位置关系是;(直接写出答案)(4)、若AC=5,BC=12,求⊙O的半径.25. 水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克.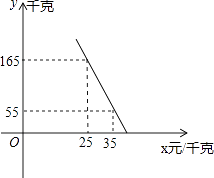 (1)、现在实际购进这种水果每千克多少元?(2)、王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系.
(1)、现在实际购进这种水果每千克多少元?(2)、王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系.①求y与x之间的函数关系式;
②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
26. 如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度.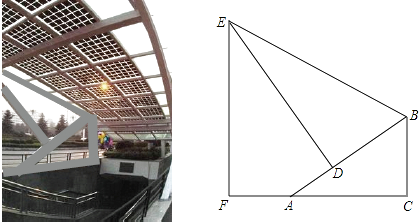 27. 阅读材料
27. 阅读材料如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
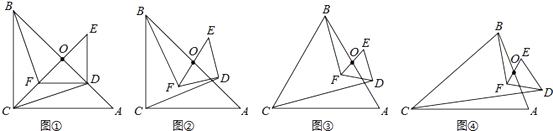 (1)、将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;(2)、如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;(3)、如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出 的值(用含α的式子表示出来)28.
(1)、将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;(2)、如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;(3)、如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出 的值(用含α的式子表示出来)28.如图①,若二次函数y= x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y= x的图象的对称点为C.
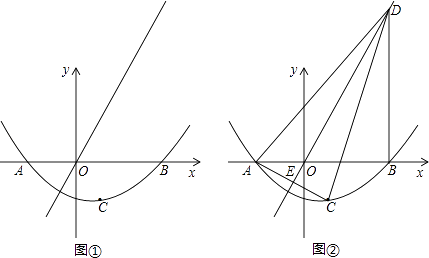 (1)、求b、c的值;(2)、证明:点C在所求的二次函数的图象上;(3)、如图②,过点B作DB⊥x轴交正比例函数y= x的图象于点D,连结AC,交正比例函数y= x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
(1)、求b、c的值;(2)、证明:点C在所求的二次函数的图象上;(3)、如图②,过点B作DB⊥x轴交正比例函数y= x的图象于点D,连结AC,交正比例函数y= x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.