2013年江苏省徐州市中考数学试卷

试卷更新日期：2017-05-22 类型：中考真卷

进入出卷网下载

一、选择题

1. $\frac{1}{2}$ 的相反数是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 下列各式的运算结果为x⁶的是（）

A、x⁹÷x³ B、（x³）³ C、x²•x³ D、x³+x³

查看试题解析
3. 2013年我市财政计划安排社会保障和公共卫生等支出约1820000000元支持民生幸福工程，该数据用科学记数法表示为（）

A、18.2×10⁸元 B、1.82×10⁹元 C、1.82×10¹⁰元 D、0.182×10¹⁰元

查看试题解析
4. 若等腰三角形的顶角为80°，则它的底角度数为（）

A、80° B、50° C、40° D、20°

查看试题解析
5. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为P．若CD=8，OP=3，则⊙O的半径为（）

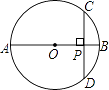A、10 B、8 C、5 D、3

查看试题解析
6. 下列函数中，y随x的增大而减小的函数是（）

A、y=2x+8 B、y=﹣2+4x C、y=﹣2x+8 D、y=4x

查看试题解析
7. 下列说法正确的是（）

A、若甲组数据的方差S_甲²=0.39，乙组数据的方差S_乙²=0.25，则甲组数据比乙组数据大 B、从1，2，3，4，5，中随机抽取一个数，是偶数的可能性比较大 C、数据3，5，4，1，﹣2的中位数是3 D、若某种游戏活动的中奖率是30%，则参加这种活动10次必有3次中奖

查看试题解析
8. 二次函数y=ax²+bx+c图象上部分点的坐标满足下表：
x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…
则该函数图象的顶点坐标为（）

A、（﹣3，﹣3） B、（﹣2，﹣2） C、（﹣1，﹣3） D、（0，﹣6）

查看试题解析

二、填空题

9. 某天的最低气温是﹣2℃，最高气温是10℃，则这天气温的极差为℃．

查看试题解析
10. 当m+n=3时，式子m²+2mn+n²的值为．

查看试题解析
11. 要使 $\sqrt{x - 2}$ 在实数范围内有意义，x应满足的条件是．

查看试题解析
12. 若∠α=50°，则它的余角是°．

查看试题解析
13. 请写出一个是中心对称图形的几何图形的名称：．

查看试题解析
14. 若两圆的半径分别是2和3，圆心距是5，则这两圆的位置关系是．

查看试题解析
15. 反比例函数y= $\frac{k}{x}$ 的图象经过点（1，﹣2），则k的值为．

查看试题解析
16. 如图，点A、B、C在⊙O上，若∠C=30°，则∠AOB的度数为°．

查看试题解析
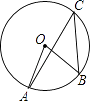17. 已知扇形的圆心角为120°，弧长为10πcm，则扇形的半径为cm．

查看试题解析
18. 如图，在正八边形ABCDEFGH中，四边形BCFG的面积为20cm² ，则正八边形的面积为cm² ．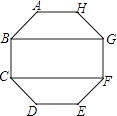

查看试题解析

三、解答题

19.

(1)、计算：|﹣2|﹣ $\sqrt{9}$ +（﹣2013）⁰；

(2)、计算：（1+ $\frac{1}{x - 1}$ ）÷ $\frac{x}{x^{2} - 1}$ ．

查看试题解析
20.

(1)、解方程：x²﹣2x=1；

(2)、解不等式组： ${\begin{matrix} 2 x + 4 \geq 0 \\ 1 - 2 x > 0 \end{matrix}$ ．

查看试题解析
21. 2012年我国国民经济运行总体平稳，全年全国公共财政收入117210亿元，2008﹣2012年全国公共财政收入及其增长速度情况如图所示：

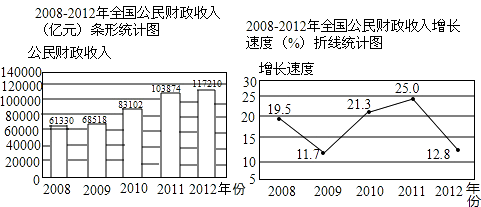(1)、这五年中全国公共财政收入增长速度最高的年份是年；

(2)、2012年的全国公共财政收入比2011年多亿元；

(3)、这五年的全国公共财政收入增长速度的平均数是．

查看试题解析
22. 一只不透明的袋子中装有白球2个和黄球1个，这些球除颜色外都相同，搅匀后从中任意摸出1个球，记下颜色后不放回，搅匀后再从中任意摸出1个球，请用列表或画树状图的方法求两次都摸出白球的概率．

查看试题解析
23. 为改善生态环境，防止水土流失，某村计划在荒坡上种1000棵树．由于青年志愿者的支援，每天比原计划多种25%，结果提前5天完成任务，原计划每天种多少棵树？

查看试题解析
24. 如图，四边形ABCD是平行四边形，DE平分∠ADC交AB于点E，BF平分∠ABC，交CD于点F．

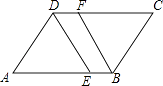(1)、求证：DE=BF；

(2)、连接EF，写出图中所有的全等三角形．（不要求证明）

查看试题解析
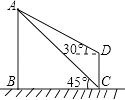
25.
如图，为了测量某风景区内一座塔AB的高度，小明分别在塔的对面一楼房CD的楼底C，楼顶D处，测得塔顶A的仰角为45°和30°，已知楼高CD为10m，求塔的高度（结果精确到0.1m）．（参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
26. 如图，在Rt△ABC中，∠C=90°，翻折∠C，使点C落在斜边AB上某一点D处，折痕为EF（点E、F分别在边AC、BC上）．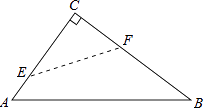

(1)、若以C、E、F为顶点的三角形与以A、B、C为顶点的三角形相似．
①当AC=BC=2时，AD的长为；
②当AC=3，BC=4时，AD的长为；

(2)、当点D是AB的中点时，△CEF与△CBA相似吗？请说明理由．

查看试题解析
27. 为增强公民的节约意识，合理利用天然气资源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：
每月用气量
单价（元/m³）
不超出75m³的部分
2.5
超出75m³不超出125m³的部分
a
超出125m³的部分
a+0.25

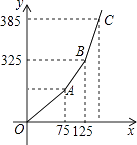(1)、若甲用户3月份的用气量为60m³ ，则应缴费元；

(2)、若调价后每月支出的燃气费为y（元），每月的用气量为x（m³），y与x之间的关系如图所示，求a的值及y与x之间的函数关系式；

(3)、在（2）的条件下，若乙用户2、3月份共用气175m³（3月份用气量低于2月份用气量），共缴费455元，乙用户2、3月份的用气量各是多少？

查看试题解析
28.
如图，二次函数y= $\frac{1}{2}$ x²+bx﹣ $\frac{3}{2}$ 的图象与x轴交于点A（﹣3，0）和点B，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接DP，过点P作DP的垂线与y轴交于点E．

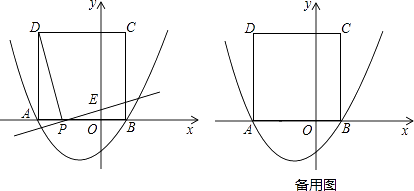(1)、请直接写出点D的坐标：；

(2)、当点P在线段AO（点P不与A、O重合）上运动至何处时，线段OE的长有最大值，求出这个最大值；

(3)、是否存在这样的点P，使△PED是等腰三角形？若存在，请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积；若不存在，请说明理由．

查看试题解析

每月用气量	单价（元/m³）
不超出75m³的部分	2.5
超出75m³不超出125m³的部分	a
超出125m³的部分	a+0.25

x	…	﹣3	﹣2	﹣1	0	1	…
y	…	﹣3	﹣2	﹣3	﹣6	﹣11	…