江苏省无锡市新吴区2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2019-05-23 类型:期中考试
一、单选题
-
1. 下列现象是数学中的平移的是( )A、小朋友荡秋千 B、碟片在光驱中运行 C、“神舟”十号宇宙飞船绕地球运动 D、瓶装饮料在传送带上移动2. 下列各式中计算正确的是( )A、 = x5 B、 C、 D、3. 如图,AB//CD,直线l 分别交 AB,CD 于 E,F,∠1=56°,则∠2 的度数是( )
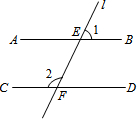 A、56° B、146° C、134° D、124°4. 如图,三角形ABC 经过平移后得到三角形 DEF,下列说法:①AB∥DE;②AD=BE;③∠ACB=∠DFE;④BC=DE.其中正确的有 ( )
A、56° B、146° C、134° D、124°4. 如图,三角形ABC 经过平移后得到三角形 DEF,下列说法:①AB∥DE;②AD=BE;③∠ACB=∠DFE;④BC=DE.其中正确的有 ( )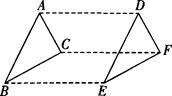 A、1 个 B、2 个 C、3 个 D、4 个5. a=-0.22 ,b=-2-2 ,c= , d= ,则它们的大小关系是( )A、a < b < c < d B、b < a < d < c C、a < d < c < b D、c < a < d < b6. 有 4 根小木棒,长度分别为 2cm、3cm、4cm、5 cm 任意取其中的 3 根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为 ( )A、1 个 B、2 个 C、3 个 D、4 个7. 如图,在边长为 a 的正方形上剪去一个边长为b 的小正方形( a > b ),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是 ( )
A、1 个 B、2 个 C、3 个 D、4 个5. a=-0.22 ,b=-2-2 ,c= , d= ,则它们的大小关系是( )A、a < b < c < d B、b < a < d < c C、a < d < c < b D、c < a < d < b6. 有 4 根小木棒,长度分别为 2cm、3cm、4cm、5 cm 任意取其中的 3 根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为 ( )A、1 个 B、2 个 C、3 个 D、4 个7. 如图,在边长为 a 的正方形上剪去一个边长为b 的小正方形( a > b ),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是 ( )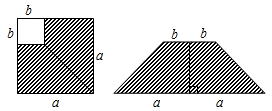 A、a2 - b2 = (a + b)(a - b) B、(a + b)2 = a2 + 2ab + b2 C、(a - b)2 = a2 - 2ab + b2 D、a2 - ab = a(a - b)8. 若 , ,则M与N的关系为A、 B、 C、 D、M与N的大小由x的取值而定9. 如图,若 AB∥CD,则α、β、θ 之间的关系为( )
A、a2 - b2 = (a + b)(a - b) B、(a + b)2 = a2 + 2ab + b2 C、(a - b)2 = a2 - 2ab + b2 D、a2 - ab = a(a - b)8. 若 , ,则M与N的关系为A、 B、 C、 D、M与N的大小由x的取值而定9. 如图,若 AB∥CD,则α、β、θ 之间的关系为( ) A、α + β + θ = 360° B、α - β + θ = 180° C、α + β - θ = 180° D、α + β + θ = 180°10. 如图,∠ABC>∠ADC,且∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E,则∠AEC与∠ADC,∠ABC 之间存在的等量关系是( )
A、α + β + θ = 360° B、α - β + θ = 180° C、α + β - θ = 180° D、α + β + θ = 180°10. 如图,∠ABC>∠ADC,且∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E,则∠AEC与∠ADC,∠ABC 之间存在的等量关系是( )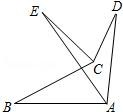 A、∠AEC=∠ABC﹣2∠ADC B、∠AEC= C、∠AEC= ∠ABC﹣∠ADC D、∠AEC=
A、∠AEC=∠ABC﹣2∠ADC B、∠AEC= C、∠AEC= ∠ABC﹣∠ADC D、∠AEC=二、填空题
-
11. 计算:(1)、 =;(2)、x3 ·x=;
(3)、x(2x-3)=;(4)、(a+2b)²=.12. 最薄的金箔的厚度为 ,用科学记数法表示为 .13. 若一个正多边形的每一个外角都是30°,则这个正多边形的边数为 .14. 若 ,则 的值为.15. 如图,把ΔABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠B=50°,则∠BDF=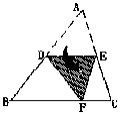 16. 如果二次三项式 x²- 2mx + 4 是一个完全平方式,那么m 的值是.17. 已知a + b = 3 , ab = -1,则(a-b)²=.18. 当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为1000 , 那么这个“特征三角形”的最小内角的度数为.19. 已知 = 1,则 x =()20. 如图, △ABC 的面积为 12,BD=2DC,AE=2EC,那么阴影部分的面积是 .
16. 如果二次三项式 x²- 2mx + 4 是一个完全平方式,那么m 的值是.17. 已知a + b = 3 , ab = -1,则(a-b)²=.18. 当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为1000 , 那么这个“特征三角形”的最小内角的度数为.19. 已知 = 1,则 x =()20. 如图, △ABC 的面积为 12,BD=2DC,AE=2EC,那么阴影部分的面积是 .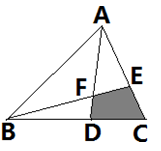
三、解答题
-
21. 计算或化简(1)、∣-1∣ + + -(2)、3a3 ×2a6 -3a12÷a3
(3)、 +(x-y)(x+2y)(4)、(3a+b-2)(3a-b+2)(5)、(3a+2)²(3a-2)²(6)、786²-786×172+86²
22. 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.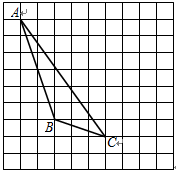 (1)、画出△ABC向右平移4个单位后得到的△A1B1C1;(2)、图中AC与A1C1的关系是:.(3)、画出△ABC的AB边上的高CD;垂足是D;(4)、图中△ABC的面积是.23. 已知:(x+a)(x-2)的结果中不含关于字母x的一次项,先化简再求(a+1)2-(2-a)(-a-2)的值.24. 已知 = , = 求 + .25.
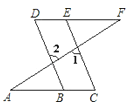
(1)、画出△ABC向右平移4个单位后得到的△A1B1C1;(2)、图中AC与A1C1的关系是:.(3)、画出△ABC的AB边上的高CD;垂足是D;(4)、图中△ABC的面积是.23. 已知:(x+a)(x-2)的结果中不含关于字母x的一次项,先化简再求(a+1)2-(2-a)(-a-2)的值.24. 已知 = , = 求 + .25.如图,∠1=∠2,∠C=∠D.∠A与∠F有怎样的数量关系?请说明理由.
 26. 阅读下列材料:
26. 阅读下列材料:“a2≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
x2+4x+5=x2+4x+4+1=(x+2)2+1,
∵(x+2)2≥0,
∴(x+2)2+1≥1,
∴x2+4x+5≥1.
试利用“配方法”解决下列问题:
(1)、填空:x2-4x+5=(x)2+;(2)、已知x2-4x+y2+2y+5=0,求x+y的值;(3)、比较代数式x2-1与2x-3的大小.27. 如图①,△ABC的角平分线BD,CE相交于点P.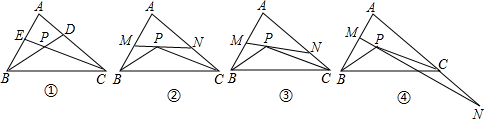 (1)、如果∠A=80∘ , 求∠BPC=.(2)、如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示).(3)、将直线MN绕点P旋转。
(1)、如果∠A=80∘ , 求∠BPC=.(2)、如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示).(3)、将直线MN绕点P旋转。(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。