江苏省常熟市2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2019-05-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $a + a^{2} = a^{3}$ B、 $2 a^{2} - a^{2} = 2$ C、 ${(a b^{2})}^{2} = a^{2} b^{4}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
2. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025m用科学记数法表示为（）

A、 $0.25 \times 10^{- 5}$ B、 $2.5 \times 10^{- 6}$ C、 $25 \times 10^{- 7}$ D、 $250 \times 10^{- 8}$

查看试题解析
3. 下列长度的三条线段能组成三角形的是（）

A、5cm，6cm，11cm B、1cm，3cm，5cm C、2cm，3cm，6cm D、3cm，4cm，5cm

查看试题解析
4. 如图， $a ∥ b$ ，射线AB分别交直线 $a ， b$ 于点B，C，点D在直线 $a$ 上，若∠A=30°，∠1=45°，则∠2的度数为（）

A、20° B、30° C、15° D、80°

查看试题解析
5. 若 $(x - 3) (2 x + m) = 2 x^{2} + n x - 15$ ，则（）

A、 $m = - 5 ， n = 1$ B、 $m = 5 ， n = - 1$ C、 $m = - 5 ， n = - 1$ D、 $m = 5 ， n = 1$

查看试题解析
6. 下列各式中，能用完全平方公式因式分解的是（）

A、 $y^{2} - x^{2} + 2 x y$ B、 $x^{2} + y^{2} + x y$ C、 $25 y^{2} + 15 y + 9$ D、 $4 x^{2} + 9 - 12 x$

查看试题解析
7. 如图，点D在△ABC内，且∠BDC=120°，∠1+∠2=55°，则∠A的度数为（）

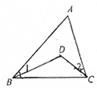A、50° B、60° C、65° D、75°

查看试题解析
8. 若 $2 x^{| k |} + (k - 1) y = 3$ 是关于 $x ， y$ 的二元一次方程，则 $k$ 的值为（）

A、-1 B、1 C、1或-1 D、0

查看试题解析
9. 两个边长分别为 $a ， b ， c$ 的直角三角形和一个两条直角边都是 $c$ 的直角三角形拼成如图所示的图形，用两种不同的计算方法计算这个图形的面积，则可得等式为（）

A、 ${(a + b)}^{2} = c^{2}$ B、 ${(a - b)}^{2} = c^{2}$ C、 $a^{2} + b^{2} = c^{2}$ D、 $a^{2} - b^{2} = c^{2}$

查看试题解析
10. 小明一笔画成了如图所示的图形，则∠A+∠B＋∠C+∠D+∠E+∠F+∠G的度数为（）

A、360° B、540° C、600° D、720°

查看试题解析

二、填空题

11. 计算： $2 x^{2} y \cdot 3 x y^{2} =$ .

查看试题解析
12. 等腰三角形的两边长分别为3 cm和7 cm，则它的周长为cm。

查看试题解析
13. 若多项式 $m^{2} - k m n + \frac{1}{4} n^{2}$ 是一个完全平方式，则 $k$ 的值为.

查看试题解析
14. 如果一个多边形的每一个角都相等，且一个内角是它相邻外角的4倍，则该多边形的边数是.

查看试题解析
15. 如果 $(x + 1) (x^{2} - 5 a x + a)$ 的乘积中不含 $x^{2}$ 项，则 $a$ 为.

查看试题解析
16. 已知 $2 a + 3 b - 5 = 0$ ，则 $4^{a} \times 8^{b} \div 2^{2}$ 的值为.

查看试题解析
17. 已知 ${\begin{matrix} x = 2 \\ y = - 3 \end{matrix}$ 是方程组 $\{\begin{cases} a x + b y = 2 \\ b x + a y = 3 \end{cases}$ 的解，则 $a^{2} {-b}^{2}$ =.

查看试题解析
18. 如图，AD是△ABC的中线，点E在AB上，且BE=3AE，设四边形BEFD的面积为 $S_{1}$ ，△ACF的面积为 $S_{2}$ ，若 $S_{1} - S_{2} = 5$ ，则△ABC的面积为.

查看试题解析

三、解答题

19. 计算：

(1)、 $π^{0} - {(- \frac{1}{2})}^{- 2} + {(- 3)}^{2}$ ；

(2)、 $2 a^{4} - a \cdot a^{3} + {(2 a^{3})}^{2} \div a^{2}$ ；

(3)、 ${(x - \frac{1}{2} y)}^{2} - (x - \frac{1}{2} y) (x + \frac{1}{2} y)$

查看试题解析
20. 分解因式：

(1)、 $3 a^{2} - 6 a + 3 ；$

(2)、 $a^{2} - a b - 6 b^{2}$ ；

(3)、 $9 a^{2} (2 x - y) + (y - 2 x)$ ；

查看试题解析
21. 解方程组：

(1)、 ${\begin{matrix} 2 x + y = 3 \\ \frac{x + 1}{3} = \frac{1 - y}{2} \end{matrix}$

(2)、 ${\begin{matrix} x + y = - 1 \\ x - y - z = 7 \\ 2 x - y - z = 0 \end{matrix}$

查看试题解析
22. 先化简，再求值： $(1 - x) (1 + 2 x) - (2 - x) (2 + x) + 3 {(x + 1)}^{2} ，$ 其中 $x = - 2$ .

查看试题解析
23. 在如图所示的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在正方形网格的格点（网格线的交点）上.

(1)、①画出△ABC向左平移3格，再向上平移2格所得的△A₁B₁C₁；
②画出△ABC的中线CD和高AH；

(2)、求△A₁B₁C₁的面积.

查看试题解析
24. 一副直角三角板如图摆放，其中∠C=30°，∠F=45°，EF∥AC，AB与DE相交于点G，BC与EF、DF分别相交于点M、N，连接DM，交AC于点P.

(1)、求∠MND的度数；

(2)、当∠DPC=∠MNF时，DM是∠EMC的平分线吗？为什么？

查看试题解析
25. 已知，关于 $x ， y$ 的二元一次方程组 ${\begin{matrix} 2 x - 3 y = 7 a - 9 \\ x + 2 y = - 1 \end{matrix}$ 的解满足方程 $2 x - y = 8$ ，求 $a$ 的值.

查看试题解析
26. 已知 $a + b = 3 ， a b = \frac{5}{4}$ ，求下列式子的值：

(1)、 $a^{2} + b^{2} ；$

(2)、 ${(a - b)}^{2} ；$

(3)、 $2 - 2 b^{2} + 6 b$ .

查看试题解析
27.

(1)、如图，在四边形ABCD中，DE平分∠ADC，CE平分∠DCB.若∠A+∠B=140°，求∠DEC的度数；

(2)、如图，四边形ABCD沿MN折叠，使点C、D落在四边形ABCD内的点C′、D′处，探索∠AMD′、∠BNC′与∠A+∠B之间的数量关系，并说明理由；

(3)、如图，将四边形ABCD沿着直线MN翻折，使得点D落在四边形ABCD外部的D′处，点C落在四边形ABCD内部的C′处，写出∠AMD′、∠BNC′与∠A+∠B之间的关系.

查看试题解析
28. 在△ABC中，点D为边BC上一点，请回答下列问题：

(1)、如图，若∠DAC=∠B，△ABC的角平分线CE交AD于点F.试说明∠AEF=∠AFE；

(2)、在（1）的条件下，如图，△ABC的外角∠ACQ的角平分线CP交BA的延长线于点P，∠P与∠CFD有怎样的数量关系？为什么？

查看试题解析