湖北省鄂州市梁子湖区2018届九年级下学期数学期中考试卷
试卷更新日期:2019-05-23 类型:期中考试
一、单选题
-
1. 如图,立体图形的左视图是( )
 A、
A、 B、
B、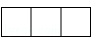 C、
C、 D、
D、 2. 2017年,是鄂州市全面建设社会主义现代化国际航空大都市的开局之年,全年全市完成地区生产总值905.92亿元,将“905.92亿”用科学记数法表示为( )A、 B、 C、 D、3. 如图,下列条件中不能判断l1∥l2的是( )
2. 2017年,是鄂州市全面建设社会主义现代化国际航空大都市的开局之年,全年全市完成地区生产总值905.92亿元,将“905.92亿”用科学记数法表示为( )A、 B、 C、 D、3. 如图,下列条件中不能判断l1∥l2的是( ) A、 B、 C、 D、4. 下列命题中假命题是( )A、六边形的外角和为 B、圆的切线垂直于过切点的半径 C、点 关于x轴对称的点为 D、抛物线 的对称轴为直线5. 已知A组四人的成绩分别为90、60、90、60,B组四人的成绩分别为70、80、80、70,用下列哪个统计知识分析区别两组成绩更恰当( )
A、 B、 C、 D、4. 下列命题中假命题是( )A、六边形的外角和为 B、圆的切线垂直于过切点的半径 C、点 关于x轴对称的点为 D、抛物线 的对称轴为直线5. 已知A组四人的成绩分别为90、60、90、60,B组四人的成绩分别为70、80、80、70,用下列哪个统计知识分析区别两组成绩更恰当( )
A、平均数 B、中位数 C、众数 D、方差6. 如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y= (m≠0)的图象相交于点A(-2,3),B(6,-1),则不等式kx+b> 的解集为( ) A、 B、 或 C、 D、 或7. 如图,△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,BM,CN交于点O,连接MN.下列结论:①∠AMN=∠ABC;②图中共有8对相似三角形;③BC=2MN.其中正确的个数是( )
A、 B、 或 C、 D、 或7. 如图,△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,BM,CN交于点O,连接MN.下列结论:①∠AMN=∠ABC;②图中共有8对相似三角形;③BC=2MN.其中正确的个数是( ) A、1个 B、2个 C、3个 D、0个8. 已知:抛物线y=ax2+bx+c(a<0)经过点(-1,0),且满足4a+2b+c>0,以下结论:①a+b>0;②a+c>0;③-a+b+c>0;④b2-2ac>5a2 , 其中正确的个数有( )A、1个 B、2个 C、3个 D、4个9. 如图,△ABC为⊙O的内接等边三角形,BC=12,点D为 上一动点,BE⊥OD于E,当点D由点B沿 运动到点C时,线段AE的最大值是( )
A、1个 B、2个 C、3个 D、0个8. 已知:抛物线y=ax2+bx+c(a<0)经过点(-1,0),且满足4a+2b+c>0,以下结论:①a+b>0;②a+c>0;③-a+b+c>0;④b2-2ac>5a2 , 其中正确的个数有( )A、1个 B、2个 C、3个 D、4个9. 如图,△ABC为⊙O的内接等边三角形,BC=12,点D为 上一动点,BE⊥OD于E,当点D由点B沿 运动到点C时,线段AE的最大值是( ) A、 B、2 C、6 D、
A、 B、2 C、6 D、二、填空题
-
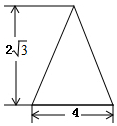
10. 分解因式:2m3-8m2+8m=.11. 阅读理解:引入新数i,新数i满足分配律、结合律、交换律,已知i2=﹣1,那么(1+i)•(1﹣i)的平方根是 .12. 关于x的不等式组 的解集中至少有5个整数解,则正数a的最小值是.13. 如图,是一圆锥的主视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的度数为.
 14. 已知等边三角形ABC在平面直角坐标系中的位置如图所示,C(1,0),点A在y轴的正半轴上,把等边三角形ABC沿x轴正半轴作无滑动的连续翻转,每次翻转120°,经过2018次翻转之后,点C的坐标是.
14. 已知等边三角形ABC在平面直角坐标系中的位置如图所示,C(1,0),点A在y轴的正半轴上,把等边三角形ABC沿x轴正半轴作无滑动的连续翻转,每次翻转120°,经过2018次翻转之后,点C的坐标是. 15. 如图,AB=BC=2,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,则BE的长为.
15. 如图,AB=BC=2,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,则BE的长为.
三、解答题
-
16. 先化简,再求值: ÷( -x+1),其中x=2sin45°-( -1)0.17. 如图,将▱ABCD沿其对角线AC折叠,使△ABC落在AEC处,CE与AD交于点F,连接DE.
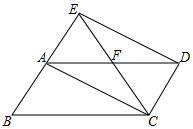 (1)、请你判断AC,DE的位置关系,并说明理由;(2)、若折叠后,CE平分AD,AB=4,BC=6,请利用(1)中的结论,求▱ABCD的面积.18. 为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
(1)、请你判断AC,DE的位置关系,并说明理由;(2)、若折叠后,CE平分AD,AB=4,BC=6,请利用(1)中的结论,求▱ABCD的面积.18. 为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。组别
分数段
频次
频率
A
60⩽x<70
17
0.17
B
70⩽x<80
30
a
C
80⩽x<90
b
0.45
D
90⩽x<100
8
0.08
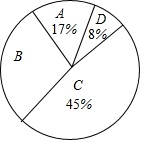
请根据所给信息,解答以下问题:
(1)、表中a= , b=;(2)、请计算扇形统计图中B组对应扇形的圆心角的度数;(3)、已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。19. 关于x的一元二次方程x2+(2k+1)x+k2=0①有两个不等的实数根.(1)、求k的取值范围;(2)、若方程①的两根的平方和为7,求k的值.20. 鄂州市电信部门积极支持鄂州国际航空大都市的建设,如图,计划修建一条连接B,C两地的电缆,测量人员在山脚A测得B,C两地的仰角分别为31°和45°,在B处测得C处的仰角为53°.已知C地比A地高50m,则电缆BC至少需要多少米?(精确到1m,参考数据:sin31°≈ ,tan31°≈ ,sin37°≈0.6,cos37°≈0.8) 21. 如图,△ABC中,AC=BC,点I是△ABC的内心,点O在边BC上,以点O为圆心,OB长为半径的圆恰好经过点I,连接CI,BI.
21. 如图,△ABC中,AC=BC,点I是△ABC的内心,点O在边BC上,以点O为圆心,OB长为半径的圆恰好经过点I,连接CI,BI. (1)、求证:CI是⊙O的切线;(2)、若AC=BC=5,AB=6,求BI的长.22. 为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1= ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
(1)、求证:CI是⊙O的切线;(2)、若AC=BC=5,AB=6,求BI的长.22. 为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1= ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:x(m2)
100
200
300
y2(元)
3900
7600
11100
 (1)、请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;(2)、设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;(3)、若种草部分的面积不少于600m2 , 栽花部分的面积不少于200m2 , 请求出绿化总费用W的最小值.23. 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(3,0),B(﹣5,0),C(0,﹣5)三点,O为坐标原点.
(1)、请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;(2)、设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;(3)、若种草部分的面积不少于600m2 , 栽花部分的面积不少于200m2 , 请求出绿化总费用W的最小值.23. 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(3,0),B(﹣5,0),C(0,﹣5)三点,O为坐标原点. (1)、求此抛物线的解析式;(2)、把抛物线y=ax2+bx+c(a≠0)向上平移 个单位长度,再向左平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;(3)、设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.
(1)、求此抛物线的解析式;(2)、把抛物线y=ax2+bx+c(a≠0)向上平移 个单位长度,再向左平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;(3)、设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.