江苏省江阴市澄要片2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2019-05-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 为了了解2018年我市七年级学生期末考试的数学成绩，从中随机抽取了1000名学生的数学成绩进行分析，下列说法正确的是（）

A、2018年我市七年级学生是总体 B、样本容量是1000 C、1000名七年级学生是总体的一个样本 D、每一名七年级学生是个体

查看试题解析
3. 代数式 $- \frac{3 x}{2}, \frac{4}{x - y}, x + y, \frac{x^{2} + 1}{π}, \frac{7}{8}, \frac{5 b}{3 a}$ 中是分式的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列二次根式中属于最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{\frac{3}{2}}$ C、 $\sqrt{7}$ D、 $\sqrt{81}$

查看试题解析
5. 若 $\frac{2 x}{x^{2} + y^{2}}$ 中的 $x$ 和 $y$ 的值都缩小2倍,则分式的值（）

A、缩小2倍 B、缩小4倍 C、扩大2倍 D、扩大4倍

查看试题解析
6. 下列说法中错误的是（）

A、对角线相等的四边形是矩形 B、两组对边分别相等的四边形是平行四边形 C、矩形的对角线相等 D、平行四边形的对边相等

查看试题解析
7. 某工程队准备修建一条长1200m的道路，由于采用新的施工方式，实际每天修建道路的速度比原计划快20%，结果提前2天完成任务.若设原计划每天修建道路xm，则根据题意可列方程为（　　）

A、 $\frac{1200}{(1 - 20 %) x} - \frac{1200}{x} = 2$ B、 $\frac{1200}{(1 + 20 %) x} - \frac{1200}{x} = 2$ C、 $\frac{1200}{x} - \frac{1200}{(1 - 20 %) x} = 2$ D、 $\frac{1200}{x} - \frac{1200}{(1 + 20 %) x} = 2$

查看试题解析
8. 已知平行四边形ABCD中，∠B=4∠A，则∠C= （）

A、36° B、72° C、144° D、36°或144°

查看试题解析
9. 如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则S_△_ECF的值为（）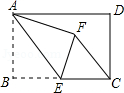

A、 $\frac{54}{25}$ B、 $\frac{72}{25}$ C、 $\frac{96}{25}$ D、 $\frac{108}{25}$

查看试题解析
10. 如图，在等边△ABC中，AB＝9，N为AB上一点，且AN＝3，BC的高线AD交BC于点D，M是AD上的动点，连结BM，MN，则BM+MN的最小值是（）

A、 $6 \sqrt{2}$ B、 $\frac{9 \sqrt{3}}{2}$ C、 $3 \sqrt{7}$ D、4 $\sqrt{7}$

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{2 x - 4}$ 有意义，则 $x$ 的取值范围是.

查看试题解析
12. 若分式 $\frac{x - 3}{x}$ 的值为0，则x的值等于．

查看试题解析
13. 一个菱形的两条对角线长分别为3cm，4cm，这个菱形的面积S=.

查看试题解析
14. 若最简二次根式 $\sqrt{2 x - 1}$ 与 $\sqrt{3}$ 是同类二次根式，则x＝.

查看试题解析
15. 关于 $x$ 的方程 $\frac{2 x - a}{x - 1} = 1$ 的解是正数，则 $a$ 的取值范围是.

查看试题解析
16. 若▱ABCD中一内角平分线和某边相交把这条边分成1cm、2cm的两条线段，则口ABCD的周长是 $cm$

查看试题解析
17. 如图，矩形内有两个相邻的正方形，面积分别为3和27，那么图中阴影部分的面积为。

查看试题解析
18. 如图1，边长为a的正方形发生形变后成为边长为a的菱形，如果这个菱形的一组对边之间的距离为h，我们把 $\frac{a}{h}$ 的值叫做这个菱形的“形变度”.例如，当形变后的菱形是如图2形状（被对角线BD分成2个等边三角形），则这个菱形的“形变度”为2： $\sqrt{3}$ .如图3，正方形由16个边长为1的小正方形组成，形变后成为菱形，△AEF（A、E、F是格点）同时形变为△A′E′F′，若这个菱形的“形变度”k＝ $\frac{16}{15}$ ，则S_△_A′E′F′＝

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{24} + | 2 - \sqrt{6} | + {(\sqrt{2})}^{2}$ ；

(2)、 $\frac{6 + 2 \sqrt{3}}{\sqrt{3}} + (2 + \sqrt{3}) (2 - \sqrt{3})$ .

查看试题解析
20.

(1)、计算： $\frac{2 x^{2}}{x + y}$ －x＋y；

(2)、解方程： $\frac{x + 3}{x} - \frac{2}{x - 2}$ ＝1.

查看试题解析
21. 化简代数式(2m- $\frac{4 m}{m + 1}$ )÷ $\frac{m^{2} - 2 m + 1}{m^{2} - 1}$ ，并求当m＝2019－2 $\sqrt{5}$ 时此代数式的值.

查看试题解析
22. 已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE.

求证：

(1)、△AFD≌△CEB.

(2)、四边形ABCD是平行四边形.

查看试题解析

23. 某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题：

初中毕业生视力抽样调查频数分布表

视力	频数（人）	频率
4.0≤x＜4.3	20	0.1
4.3≤x＜4.6	40	0.2
4.6≤x＜4.9	70	0.35
4.9≤x＜5.2	a	0.3
5.2≤x＜5.5	10	b

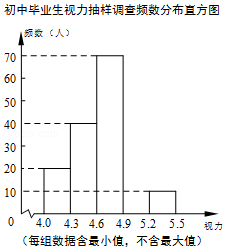(1)、本次调查样本容量为；

(2)、在频数分布表中，a＝， b＝，并将频数分布直方图补充完整；

(3)、若视力在4.9以上（含4.9）均属标准视力，根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人？

查看试题解析

24. 如图，正方形网格中，每个小方格都是边长为1的正方形，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：

(1)、△ABC的面积为；

(2)、①将△ABC绕原点O 旋转180°，画出旋转后的△A₁B₁C₁；
②将△ABC向右平移4个单位长度，画出平移后的△A₂B₂C₂；

(3)、△A₁B₁C₁与△A₂B₂C₂成中心对称吗？若是，请直接写出对称中心的坐标：.

查看试题解析
25. 在进行二次根式化简时，我们有时会碰上如 $\frac{5}{\sqrt{3}}$ ， $\sqrt{\frac{2}{3}}$ ， $\frac{2}{\sqrt{3} + 1}$ 一样的式子，其实我们还可以将其进一步化简： $\frac{5}{\sqrt{3}} = \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5 \sqrt{3}}{3}$ ， $\sqrt{\frac{2}{3}} = \sqrt{\frac{2 \times 3}{3 \times 3}} = \frac{\sqrt{6}}{3}$ ， $\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 \times (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1$
以上这种化简的步骤叫做分母有理化. $\frac{2}{\sqrt{3} + 1}$ 还可以用以下方法化简： $\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{{(\sqrt{3})}^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$

(1)、请用不同的方法化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ；

(2)、化简： $\frac{1}{\sqrt{3 + 1}} + \frac{1}{\sqrt{5} + \sqrt{2}} + \frac{1}{\sqrt{7} + \sqrt{5}} + \dots + \frac{1}{\sqrt{2 n + 1} + \sqrt{2 n - 1}}$ .

查看试题解析
26. 某修理厂需要购进甲、乙两种配件，经调查，每个甲种配件的价格比每个乙种配件的价格少0.4万元，且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.

(1)、求每个甲种配件、每个乙种配件的价格分别为多少万元；

(2)、现投入资金80万元，根据维修需要预测，甲种配件要比乙种配件至少要多22件，问乙种配件最多可购买多少件.

查看试题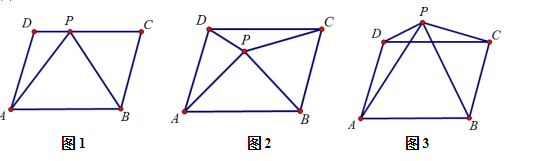解析
27. 如图，

(1)、如图 1，若 P是口ABCD 边 CD 上任意一点，连结 AP、BP，若△APB 的面积为 60 ，△APD的面积为 18，则 S△APC=.

(2)、如图 2，①若点 P 运动到口ABCD 内一点时，试说明 S△APB +S△DPC =S△BPC +S△APD.
②若此时△APB 的面积为 60，△APD 的面积为 18，则 S△APC=.

(3)、如图3，①利用（2）中的方法你会发现，S△APB ，S△DPC ，S△BPC ，S△APD 之间存在怎样的关系：.
②若此时△APB 的面积为 60，△APD 的面积为 18，请利用你的发现，求 S△APC 的面积？

查看试题解析
28. 在矩形ABCD中，AB＝3，BC＝2，以点A为旋转中心，逆时针旋转矩形ABCD，旋转角为α（0°＜α＜180°），得到矩形AEFG，点B、点C、点D的对应点分别为点E、点F、点G.

(1)、如图①，当点E落在DC边上时，直写出线段EC的长度为；

(2)、如图②，当点E落在线段CF上时，AE与DC相交于点H，连接AC，
①求证：△ACD≌△CAE；

②直接写出线段DH的长度为.

(3)、如图③设点P为边FG的中点，连接PB，PE，在矩形ABCD旋转过程中，△BEP的面积是否存在最大值？若存在请直接写出这个最大值；若不存在请说明理由.

查看试题解析