浙教版2019年数学中考模拟试卷10
试卷更新日期:2019-05-23 类型:中考模拟
一、选择题(共12小题)
-
1. 在﹣2,0, ,2四个数中,最小的是( )A、﹣2 B、0 C、 D、22. 2017年,全国参加汉语考试的人数约为6500000,将6500000用科学记数法表示为( )A、 6.5×105 B、6.5×106 C、6.5×107 D、65×1053. 下列运算结果正确的是( )A、a3•a2=a5 B、(a3)2=a5 C、a3+a2=a5 D、a﹣2=﹣a24. 抛物线y=3(x﹣2)2+5的顶点坐标是( )A、(﹣2,5) B、(﹣2,﹣5) C、(2,5) D、(2,﹣5)5. 已知不等式组 ,其解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 6. 如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
6. 如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )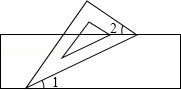 A、14° B、15° C、16° D、17°7. 在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )A、(4,﹣3) B、(﹣4,3) C、(﹣3,4) D、(﹣3,﹣4)8. 在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A、9人 B、10人 C、11人 D、12人9. 对于反比例函数y=﹣ ,下列说法不正确的是( )A、图象分布在第二、四象限 B、当x>0时,y随x的增大而增大 C、图象经过点(1,﹣2) D、若点A(x1 , y1),B(x2 , y2)都在图象上,且x1<x2 , 则y1<y210. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣ ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
A、14° B、15° C、16° D、17°7. 在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )A、(4,﹣3) B、(﹣4,3) C、(﹣3,4) D、(﹣3,﹣4)8. 在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A、9人 B、10人 C、11人 D、12人9. 对于反比例函数y=﹣ ,下列说法不正确的是( )A、图象分布在第二、四象限 B、当x>0时,y随x的增大而增大 C、图象经过点(1,﹣2) D、若点A(x1 , y1),B(x2 , y2)都在图象上,且x1<x2 , 则y1<y210. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣ ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( ) A、1个 B、2个 C、3个 D、4个11. 一次函数y=ax+b和反比例函数y= 在同一直角坐标系中的大致图象是( )A、
A、1个 B、2个 C、3个 D、4个11. 一次函数y=ax+b和反比例函数y= 在同一直角坐标系中的大致图象是( )A、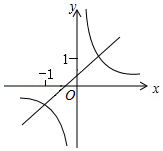 B、
B、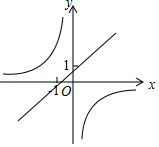 C、
C、 D、
D、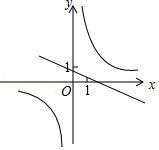 12. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1 , 第2次移动到A2 , …,第n次移动到An.则△OA2A2018的面积是( )
12. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1 , 第2次移动到A2 , …,第n次移动到An.则△OA2A2018的面积是( ) A、504m2 B、 m2 C、505 m2 D、1009m2
A、504m2 B、 m2 C、505 m2 D、1009m2二、填空题(共6小题)
-
13. 写出一个数,使这个数的绝对值等于它的相反数: .14. 习近平同志在党的十九大报告中强调,生态文明建设功在当代,利在千秋.55年来,经过三代入的努力,河北塞罕坝林场有林地面积达到1120000亩.用科学记数法表示1120000是.15. 如图.在△ABC中,∠A=60°,BC=5cm.能够将△ABC完全覆盖的最小圆形纸片的直径是cm.
 16. 任何一个无限循环小数都可以写成分数的形式,应该怎样写呢?我们以无限循环小数0. 为例进行说明:设0. =x,由0. =0.7777…可知,10x=7.7777…,所以10x﹣x=7,解方程,得x= ,于是.得0. = .将0. 写成分数的形式是.17. 如图,直线AB与双曲线y= (k<0)交于点A,B,点P是直线AB上一动点,且点P在第二象限.连接PO并延长交双曲线于点C.过点P作PD⊥y轴,垂足为点D.过点C作CE⊥x轴,垂足为E.若点A的坐标为(﹣2,3),点B的坐标为(m,1),设△POD的面积为S1 , △COE的面积为S2 , 当S1>S2时,点P的横坐标x的取值范围为.
16. 任何一个无限循环小数都可以写成分数的形式,应该怎样写呢?我们以无限循环小数0. 为例进行说明:设0. =x,由0. =0.7777…可知,10x=7.7777…,所以10x﹣x=7,解方程,得x= ,于是.得0. = .将0. 写成分数的形式是.17. 如图,直线AB与双曲线y= (k<0)交于点A,B,点P是直线AB上一动点,且点P在第二象限.连接PO并延长交双曲线于点C.过点P作PD⊥y轴,垂足为点D.过点C作CE⊥x轴,垂足为E.若点A的坐标为(﹣2,3),点B的坐标为(m,1),设△POD的面积为S1 , △COE的面积为S2 , 当S1>S2时,点P的横坐标x的取值范围为.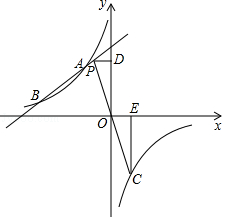 18. 如图,在平面直角坐标系中,点A1的坐标为(1,2),以点O为圆心,以OA1长为半径画弧,交直线y= x于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2 , 以O为圆心,以OA2长为半径画弧,交直线y= x于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3 , 以点O为圆心,以OA3长为半径画弧,交直线y= x于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4 , 以点O为圆心,以OA4长为半径画弧,交直线y= x于点B4 , …按照如此规律进行下去,点B2018的坐标为.
18. 如图,在平面直角坐标系中,点A1的坐标为(1,2),以点O为圆心,以OA1长为半径画弧,交直线y= x于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2 , 以O为圆心,以OA2长为半径画弧,交直线y= x于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3 , 以点O为圆心,以OA3长为半径画弧,交直线y= x于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4 , 以点O为圆心,以OA4长为半径画弧,交直线y= x于点B4 , …按照如此规律进行下去,点B2018的坐标为.
三、解答题(共8小题)
-
19. 解不等式组,并将解集在数轴上表示出来.20. 某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了 ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
21. 某地某月1~20日中午12时的气温(单位:℃)如下:
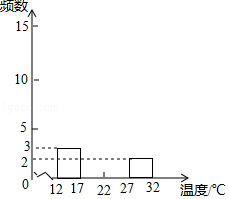 (1)、将下列频数分布表补充完整:
(1)、将下列频数分布表补充完整:气温分组
划记
频数
12≤x<17
3
17≤x<22

22≤x<27

27≤x<32

2
(2)、补全频数分布直方图;(3)、根据频数分布表或频数分布直方图,分析数据的分布情况.22. 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D,OB与⊙O相交于点E. (1)、求证:AC是⊙O的切线;(2)、若BD= ,BE=1.求阴影部分的面积.23. 甲口袋中有2个白球、1个红球,乙口袋中有1个白球、1个红球,这些球除颜色外无其他差别.分别从每个口袋中随机摸出1个球.(1)、求摸出的2个球都是白球的概率.(2)、下列事件中,概率最大的是_______.A、摸出的2个球颜色相同 B、摸出的2个球颜色不相同 C、摸出的2个球中至少有1个红球 D、摸出的2个球中至少有1个白球24. 如图,为了测量建筑物AB的高度,在D处树立标杆CD,标杆的高是2m,在DB上选取观测点E、F,从E测得标杆和建筑物的顶部C、A的仰角分别为58°、45°.从F测得C、A的仰角分别为22°、70°.求建筑物AB的高度(精确到0.1m).(参考数据:tan22°≈0.40,tan58°≈1.60,tan70°≈2.75.)
(1)、求证:AC是⊙O的切线;(2)、若BD= ,BE=1.求阴影部分的面积.23. 甲口袋中有2个白球、1个红球,乙口袋中有1个白球、1个红球,这些球除颜色外无其他差别.分别从每个口袋中随机摸出1个球.(1)、求摸出的2个球都是白球的概率.(2)、下列事件中,概率最大的是_______.A、摸出的2个球颜色相同 B、摸出的2个球颜色不相同 C、摸出的2个球中至少有1个红球 D、摸出的2个球中至少有1个白球24. 如图,为了测量建筑物AB的高度,在D处树立标杆CD,标杆的高是2m,在DB上选取观测点E、F,从E测得标杆和建筑物的顶部C、A的仰角分别为58°、45°.从F测得C、A的仰角分别为22°、70°.求建筑物AB的高度(精确到0.1m).(参考数据:tan22°≈0.40,tan58°≈1.60,tan70°≈2.75.)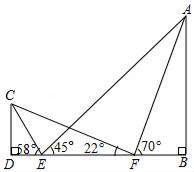 25. 已知抛物线y=x2+mx﹣2m﹣4(m>0).(1)、证明:该抛物线与x轴总有两个不同的交点;(2)、设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.
25. 已知抛物线y=x2+mx﹣2m﹣4(m>0).(1)、证明:该抛物线与x轴总有两个不同的交点;(2)、设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.
①试判断:不论m取任何正数,⊙P是否经过y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;
②若点C关于直线x=﹣ 的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求 的值.
26. 如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.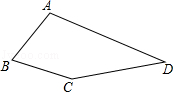 (1)、求∠A+∠C的度数;(2)、连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;(3)、若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2 , 求点E运动路径的长度.
(1)、求∠A+∠C的度数;(2)、连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;(3)、若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2 , 求点E运动路径的长度.