浙教版2019年数学中考模拟试卷9
试卷更新日期:2019-05-23 类型:中考模拟
一、选择题(共12小题)
-
1. 在0,1,﹣ ,﹣1四个数中,最小的数是( )A、0 B、1 C、- D、﹣12. 如图,直线a,b被直线c所截,那么∠1的同位角是( )
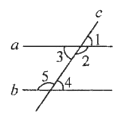 A、∠2 B、∠3 C、∠4 D、∠53. 根据衢州市统计局发布的统计数据显示,衢州市2017年全市生产总值为138000000000元,按可比价格计算,比上年增长7.3%,数据138000000000元用科学记数法表示为( )A、1.38×1010元 B、1.38×1011元 C、1.38×1012元 D、0.138×1012元4. 实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是( )
A、∠2 B、∠3 C、∠4 D、∠53. 根据衢州市统计局发布的统计数据显示,衢州市2017年全市生产总值为138000000000元,按可比价格计算,比上年增长7.3%,数据138000000000元用科学记数法表示为( )A、1.38×1010元 B、1.38×1011元 C、1.38×1012元 D、0.138×1012元4. 实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是( ) A、|a|>|b| B、|ac|=ac C、b<d D、c+d>05. 如图,直线l是一次函数y=kx+b的图象,若点A(3,m)在直线l上,则m的值是( )
A、|a|>|b| B、|ac|=ac C、b<d D、c+d>05. 如图,直线l是一次函数y=kx+b的图象,若点A(3,m)在直线l上,则m的值是( )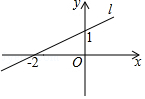 A、﹣5 B、 C、 D、76. 一个几何体的三视图如图所示,该几何体是( )
A、﹣5 B、 C、 D、76. 一个几何体的三视图如图所示,该几何体是( )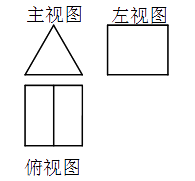 A、直三棱柱 B、长方体 C、圆锥 D、立方体7. 如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,指针停止后落在黄色区域的概率是( )
A、直三棱柱 B、长方体 C、圆锥 D、立方体7. 如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,指针停止后落在黄色区域的概率是( )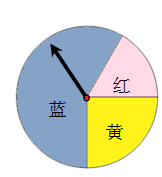 A、 B、 C、 D、8. 把不等式组 中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、
A、 B、 C、 D、8. 把不等式组 中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、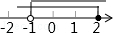 B、
B、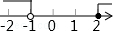 C、
C、 D、
D、 9. 在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的 后得到线段CD,则点A的对应点C的坐标为( )A、(5,1) B、(4,3) C、(3,4) D、(1,5)10. 如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )
9. 在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的 后得到线段CD,则点A的对应点C的坐标为( )A、(5,1) B、(4,3) C、(3,4) D、(1,5)10. 如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )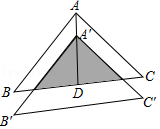 A、2 B、3 C、 D、11. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
A、2 B、3 C、 D、11. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3.其中正确的个数是( )
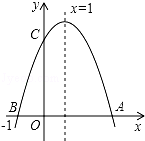 A、1 B、2 C、3 D、412. 在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
A、1 B、2 C、3 D、412. 在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )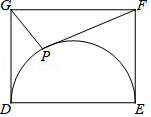 A、 B、 C、34 D、10
A、 B、 C、34 D、10二、填空题(共6小题)
-
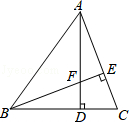
13. 在△ABC中,若∠A=30°,∠B=50°,则∠C= .14. 化简(x﹣1)(x+1)的结果是.15. 如图,△ABC的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是 .
 16. 若二元一次方程组 的解为 ,则a﹣b= .17. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S= .现已知△ABC的三边长分别为1,2, ,则△ABC的面积为 .
16. 若二元一次方程组 的解为 ,则a﹣b= .17. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S= .现已知△ABC的三边长分别为1,2, ,则△ABC的面积为 . 18. 将从1开始的连续自然数按以下规律排列:
18. 将从1开始的连续自然数按以下规律排列:第1行
1
第2行
2
3
4
第3行
9
8
7
6
5
第4行
10
11
12
13
14
15
16
第5行
25
24
23
22
21
20
19
18
17
…
则2018在第行.
三、解答题(共8小题)
-
19. 计算:| ﹣2|+sin60°﹣ ﹣(﹣1 )2+2﹣220. 如图,在▱ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE=CF.
 21. 有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
21. 有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案: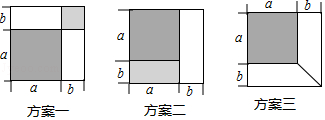
小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2 ,
对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2
请你根据方案二、方案三,写出公式的验证过程.
方案二:
方案三:
22. 如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.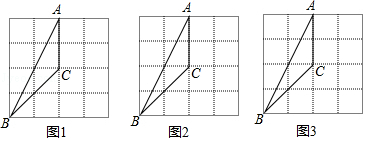 (1)、在图1中,画出一个与△ABC成中心对称的格点三角形;(2)、在图2中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;(3)、在图3中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.△DCE为所求作
(1)、在图1中,画出一个与△ABC成中心对称的格点三角形;(2)、在图2中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;(3)、在图3中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.△DCE为所求作
23. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.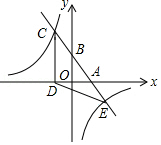 (1)、求一次函数与反比例函数的解析式;(2)、记两函数图象的另一个交点为E,求△CDE的面积;(3)、直接写出不等式kx+b≤ 的解集.24. 现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
(1)、求一次函数与反比例函数的解析式;(2)、记两函数图象的另一个交点为E,求△CDE的面积;(3)、直接写出不等式kx+b≤ 的解集.24. 现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):步数
频数
频率
0≤x<4000
8
a
4000≤x<8000
15
0.3
8000≤x<12000
12
b
12000≤x<16000
c
0.2
16000≤x<20000
3
0.06
20000≤x<24000
d
0.04
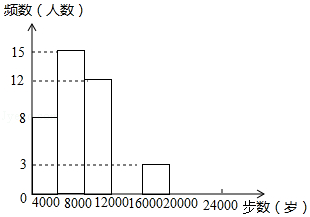
请根据以上信息,解答下列问题:
(1)、写出a,b,c,d的值并补全频数分布直方图;(2)、本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?(3)、若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.25. 如图,抛物线y=ax2+bx(a<0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.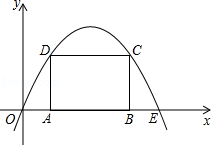 (1)、求抛物线的函数表达式.(2)、当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)、保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.26. 在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.
(1)、求抛物线的函数表达式.(2)、当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)、保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.26. 在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.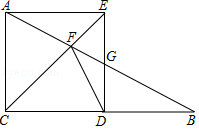 (1)、如图,点D在线段CB上,四边形ACDE是正方形.
(1)、如图,点D在线段CB上,四边形ACDE是正方形.①若点G为DE的中点,求FG的长.
②若DG=GF,求BC的长.
(2)、已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.