浙教版2019年数学中考模拟试卷8
试卷更新日期:2019-05-23 类型:中考模拟
一、选择题(共10小题)
-
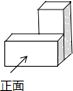
1. ﹣2的绝对值是( )A、2 B、﹣2 C、0 D、2. 2014年广东省人口数超过105000000,将105000000这个数用科学记数法表示为( )A、0.105×109 B、1.05×109 C、1.05×108 D、105×1063. 用两块完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是( )
 A、
A、 B、
B、 C、
C、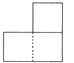 D、
D、 4. 在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其它均相同,从袋中随机摸出一个球,记下颜色后放回.通过大量重复摸球试验后发现,摸到红球的频率在25%附近摆动,则口袋中的白球可能有( )
4. 在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其它均相同,从袋中随机摸出一个球,记下颜色后放回.通过大量重复摸球试验后发现,摸到红球的频率在25%附近摆动,则口袋中的白球可能有( )
A、12个 B、13个 C、15个 D、16个5. 已知反比例函数y= 的图象经过点P(﹣1,2),则这个函数的图象位于( )A、第二,三象限 B、第一,三象限 C、第三,四象限 D、第二,四象限6. 如图所示,在平行四边形ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则 等于( ) A、 B、 C、 D、不一定7. 如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为( )
A、 B、 C、 D、不一定7. 如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为( )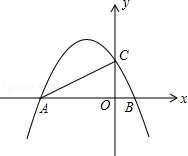 A、﹣ B、﹣ C、﹣1 D、﹣28. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1035 B、x(x﹣1)=1035×2 C、x(x﹣1)=1035 D、2x(x+1)=10359. a,b,c为常数,且(a﹣c)2>a2+c2 , 则关于x的方程ax2+bx+c=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、有一根为010. 已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )A、3﹣ 或1+ B、3﹣ 或3+ C、3+ 或1﹣ D、1﹣ 或1+
A、﹣ B、﹣ C、﹣1 D、﹣28. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1035 B、x(x﹣1)=1035×2 C、x(x﹣1)=1035 D、2x(x+1)=10359. a,b,c为常数,且(a﹣c)2>a2+c2 , 则关于x的方程ax2+bx+c=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、有一根为010. 已知二次函数y=﹣(x﹣h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为﹣5,则h的值为( )A、3﹣ 或1+ B、3﹣ 或3+ C、3+ 或1﹣ D、1﹣ 或1+二、填空题(共8小题)
-
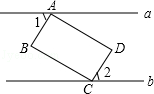
11. 分解因式:ax2﹣ay2= .12. 我国高速公路发展迅速,据报道,到目前为止,全国高速公路总里程约为10.8万千米,10.8万用科学记数法表示为 .13. 已知一个样本0,﹣1,x,1,3它们的平均数是2,则这个样本的中位数是 .14. 如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为.
 15. 如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于G,AB=6,则AG=.
15. 如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于G,AB=6,则AG=.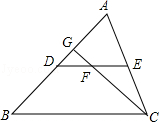 16. 如图,AB,AC分别为⊙O的内接正六边形,内接正方形的一边,BC是圆内接n边形的一边,则n等于.
16. 如图,AB,AC分别为⊙O的内接正六边形,内接正方形的一边,BC是圆内接n边形的一边,则n等于.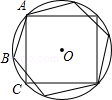 17. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=.
17. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=.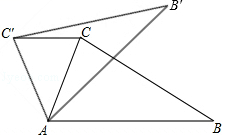 18. 如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为.
18. 如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为.
三、解答题(共8小题)
-
19. 先化简,再求值:(x+2)2﹣4x(x+1),其中x= .20. 如图,△AOB,△COD是等腰直角三角形,点D在AB上,
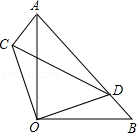 (1)、求证:△AOC≌△BOD;(2)、若AD=3,BD=1,求CD.21. 解方程: + =1.22. 在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张,不放回,再从剩下的卡片中随机抽取一张.
(1)、求证:△AOC≌△BOD;(2)、若AD=3,BD=1,求CD.21. 解方程: + =1.22. 在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张,不放回,再从剩下的卡片中随机抽取一张.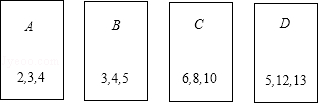 (1)、请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);(2)、我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.23. 如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数y= (x>0)图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)、请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);(2)、我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.23. 如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数y= (x>0)图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.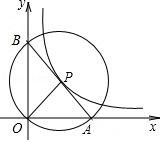 (1)、求证:P为线段AB的中点;(2)、求△AOB的面积.24. 如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
(1)、求证:P为线段AB的中点;(2)、求△AOB的面积.24. 如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB. (1)、求证:EA是⊙O的切线;(2)、已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;(3)、已知AF=4,CF=2.在(2)条件下,求AE的长.25. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)、求证:EA是⊙O的切线;(2)、已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;(3)、已知AF=4,CF=2.在(2)条件下,求AE的长.25. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.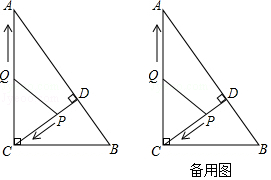 (1)、①求线段CD的长;
(1)、①求线段CD的长;②求证:△CBD∽△ABC.
(2)、设△CPQ的面积为S,求S与t之间的函数关系式,并求出S的最大值.(3)、是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,请直接写出满足条件的t的值;若不存在,请说明理由.②根据两角相等的三角形相似即可判断;
26. 在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC= ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直. (1)、如图1,当点R与点D重合时,求PQ的长;(2)、如图2,试探索: 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)、如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.
(1)、如图1,当点R与点D重合时,求PQ的长;(2)、如图2,试探索: 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)、如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.