浙教版2019年数学中考模拟试卷6
试卷更新日期：2019-05-23 类型：中考模拟
一、选择题（共10小题）
-
1. 7的算术平方根是（ ）A、 49 B、 C、﹣ D、±2. 2017年5月12日，利用微软Windows漏洞爆发的wannaCry勒索病毒，目前已席卷全球150多个国家，至少30万台电脑中招，预计造成的经济损失将达到80亿美元，世人再次领教了黑客的厉害，将数据80亿用科学记数法表示为（ ）A、8×108 B、8×109 C、0.8×109 D、0.8×10103. 如图，已知∠ABC＝∠DCB，添加以下条件，不能判定△ABC≌△DCB的是（ ）
A、∠A＝∠D B、∠ACB＝∠DBC C、AC＝DB D、AB＝DC4. 从棱长为2a的正方体零件的一角，挖去一个棱长为a的小正方体，得到一个如图所示的零件，则这个零件的俯视图是（ ）
A、
B、
C、
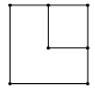D、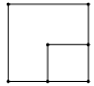
5. 二次函数y=（x﹣2）2+7的顶点坐标是（）A、（﹣2，7） B、（2，7） C、（﹣2，﹣7） D、（2，﹣7）6. 如图，∠A是⊙O的圆周角，∠A＝40°，则∠OBC＝（ ）
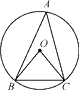A、30° B、40° C、50° D、60°7. 从下列不等式中选择一个与x+1≥2组成不等式组，使该不等式组的解集为x≥1，那么这个不等式可以是（ ）A、x＞﹣1 B、x＞2 C、x＜﹣1 D、x＜28. 如图，有一矩形纸片ABCD，AB＝6，AD＝8，将纸片折叠使AB落在AD边上，折痕为AE，再将△ABE以BE为折痕向右折叠，AE与CD交于点F，则 的值是（ ）
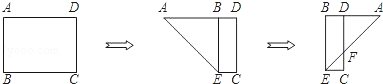A、1 B、 C、 D、9. 已知点E（2，1）在二次函数y＝x2﹣8x+m（m为常数）的图象上，则点E关于图象对称轴的对称点坐标是（ ）A、（4，1） B、（5，1） C、（6，1） D、（7，1）10. 如图，在Rt△ABC中，∠C＝90°，AC＝BC＝6cm，点P从点A出发，沿AB方向以每秒
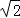cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将△PQC沿BC翻折，点P的对应点为点P′.设点Q运动的时间为t秒，若四边形QPCP′为菱形，则t的值为（ ） 
A、 B、2 C、2 D、3二、填空题（共8小题）
-
11. 分解因式：b2﹣ab+a﹣b＝.12. 分式方程 的解是 ．13. 若单项式﹣xm﹣2y3与 xny2m﹣3n的和仍是单项式，则m﹣n= ．14. 甲、乙、丙三位好朋友随机站成一排照合影，甲没有站在中间的概率为 ．15. 某学习小组为了探究函数y＝x2﹣|x|的图象和性质，根据以往学习函数的经验，列表确定了该函数图象上一些点的坐标，表格中的m＝.
x
…
﹣2
﹣1.5
﹣1
﹣0.5
0
0.5
1
1.5
2
…
y
…
2
0.75
0
﹣0.25
0
﹣0.25
0
m
2
…
16. 我们把直角坐标系中横坐标与纵坐标都是整数的点称为整点.反比例函数y＝﹣ 的图象上有一些整点，请写出其中一个整点的坐标.17. 如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；
②方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3；
③3a+c＞0；
④当y＞0时，x的取值范围是﹣1≤x＜3；
⑤当x＜0时，y随x增大而增大；
其中结论正确有.
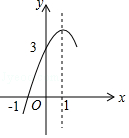18. 如图，△ABC的三个顶点分别为A（1，2），B（1，3），C（3，1），若反比例函数y＝ 在第一象限内的图象与△ABC有公共点，则k的取值范围是.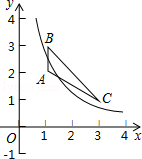
三、解答题（共7小题）
-
19. 先化简（ ﹣x）÷（1+x﹣ ），再选一个你喜欢的整数值，代入求值．20. 滴滴打车为市民的出行带来了很大的方便，小亮调查了若干市民一周内使用滴滴打车的时间t（单位：分），将获得的数据分成四组，绘制了如下统计图，请根据图中信息，解答下列问题：
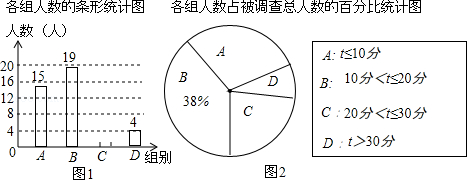(1)、这次被调查的总人数是多少？(2)、试求表示C组的扇形圆心角的度数，并补全条形统计图；(3)、若全市的总人数为666万，试求全市一周内使用滴滴打车超过20分钟的人数大约有多少？21. 如图，在昆明市轨道交通的修建中，规划在A、B两地修建一段地铁，点B在点A的正东方向，由于A、B之间建筑物较多，无法直接测量，现测得古树C在点A的北偏东45°方向上，在点B的北偏西60°方向上，BC＝400m，请你求出这段地铁AB的长度.（结果精确到1m，参考数据： ， ≈1.732）
22. 国家实施高效节能电器的财政补贴政策，某款空调在政策实施后.每购买一台，客户每购买一台可获得补贴500元.若同样用11万元所购买此款空调，补贴后可购买的台数比补贴前多20%，则该款空调补贴前的售价为每台多少元？
23. 某商品的进价为每件50元．当售价为每件70元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：
(1)、若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；
(2)、当降价多少元时，每星期的利润最大？最大利润是多少？24. 如图，AB是⊙O的直径，∠ACB的平分线交AB于点D，交⊙O于点E，过点C作⊙O的切线CP交BA的延长线于点P，连接AE.
(1)、求证：PC＝PD；(2)、若AC＝5cm，BC＝12cm，求线段AE，CE的长.25. 如图，在平面直角坐标系xOy中，A、B、C三点分别为坐标轴上的三个点，且OA＝1，OB＝3，OC＝4.
(1)、求经过A、B、C三点的抛物线的解析式；(2)、在平面直角坐标系xOy中是否存在一点P，使得以A、B、C、P为顶点的四边形为菱形？若存在，请求出点P的坐标；若不存在，请说明理由.(3)、若点M为该抛物线上一动点，在（2）的条件下，请求出当|PM﹣AM|为最大值时点M的坐标，并直接写出|PM﹣AM|的最大值.