浙教版2019年数学中考模拟试卷5
试卷更新日期:2019-05-23 类型:中考模拟
一、选择题(共10小题)
-
1. ﹣6的倒数是( )A、﹣6 B、6 C、 D、2. 11月30日,“海峡号”客滚轮直航台湾旅游首发团正式起航.“海峡号”由福建海峡高速客滚航运有限公司斥资近3亿元购进,将3亿用科学记数法表示正确的是( )A、 3×108 B、3×109 C、3×1010 D、3×10113. 一个几何体的主视图、左视图、俯视图完全相同,它一定是( )A、圆柱 B、圆锥 C、球体 D、长方体4. 在一个不透明的盒子中装有8个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为 ,则黄球的个数为( )
A、2 B、4 C、12 D、165. 下列运算正确的是( )A、(a+b)2=a2+b2 B、(﹣1+x)(﹣x﹣1)=1﹣x2 C、a4•a2=a8 D、(﹣2x)3=﹣6x 36. 一次数学检测中,有5名学生的成绩分别是86,89,78,93,90.则这5名学生成绩的平均数和中位数分别是( )A、87.2,89 B、89,89 C、87.2,78 D、90,937. 已知下列命题:①对顶角相等;②若a>b>0,则 < ;③对角线相等且互相垂直的四边形是正方形;④抛物线y=x2﹣2x与坐标轴有3个不同交点;⑤边长相等的多边形内角都相等.从中任选一个命题是真命题的概率为( )
A、 B、 C、 D、8. 若关于x的一元二次方程kx2﹣6x+9=0有两个不相等的实数根,则k的取值范围( )A、k<1且k≠0 B、k≠0 C、k<1 D、k>19. 如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:①∠BOD=90°;②DO∥AB;③CD=AD;④△BDE∽△BCD;⑤
正确的有( )
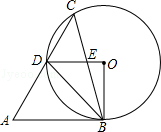 A、①② B、①④⑤ C、①②④⑤ D、①②③④⑤10. 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB= .下列结论:
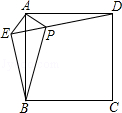
A、①② B、①④⑤ C、①②④⑤ D、①②③④⑤10. 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB= .下列结论:①△APD≌△AEB;
②点B到直线AE的距离为 ;
③EB⊥ED;
④S△APD+S△APB=1+ ;
⑤S正方形ABCD=4+ .
其中正确结论的序号是( )
 A、①③④ B、①②⑤ C、③④⑤ D、①③⑤
A、①③④ B、①②⑤ C、③④⑤ D、①③⑤二、填空题(共8小题)
-
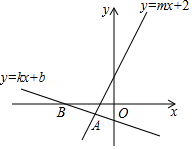
11. 分解因式:x3y﹣xy= .12. 一只不透明的袋子中装有红球和白球共30个,这些球除了颜色外都相同,校课外学习小组做摸球实验,将球搅匀后任意摸出一个球,记下颜色后放回,搅匀,通过多次重复试验,算得摸到红球的频率是0.2,则袋中有个红球.13. 如图,平面直角坐标系中,经过点B(﹣4,0)的直线y=kx+b与直线y=mx+2相交于点 ,则不等式mx+2<kx+b<0的解集为.
 14. 在平面直角坐标系中,若点P(2x+6,5x)在第四象限,则x的取值范围是 .15. 如图,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=度.
14. 在平面直角坐标系中,若点P(2x+6,5x)在第四象限,则x的取值范围是 .15. 如图,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=度.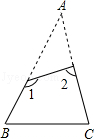 16. 已知M、N两点关于y轴对称,且点M在双曲线y= 上,点N在直线y=x+3上,设点M坐标为(a,b),则抛物线y=﹣abx2+(a+b)x的顶点坐标为.17. 在草稿纸上计算:① ;② ;③ ;④ ,观察你计算的结果,用你发现的规律直接写出下面式子的值 =.18. 如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为.
16. 已知M、N两点关于y轴对称,且点M在双曲线y= 上,点N在直线y=x+3上,设点M坐标为(a,b),则抛物线y=﹣abx2+(a+b)x的顶点坐标为.17. 在草稿纸上计算:① ;② ;③ ;④ ,观察你计算的结果,用你发现的规律直接写出下面式子的值 =.18. 如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为.
三、解答题(共8小题)
-
19. 计算: ﹣4sin45°+|﹣4|.20. 先化简,再求值: ,其中x=2.21. A,B,C三名学生竞选学校学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图1:
表一:
A
B
C
笔试
85
95
90
口试
80
85
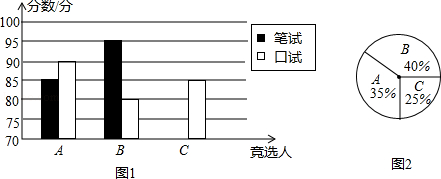
①请将表一和图一中的空缺部分补充完整.
②竞选的最后一个程序是由本学校的300名学生进行投票,三位候选人的得票情况如图2(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
22. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,Rt△ABC的顶点坐标为点A(﹣6,1),点B(﹣3,1),点C(﹣3,3).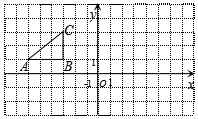 (1)、将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1 , 试在图上画出图形Rt△A1B1C1 , 并写出点A1的坐标;(2)、将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2 , 试在图上画出图形Rt△A2B2C2.并写出顶点A从开始到A2经过的路径长23. 某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)、将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1 , 试在图上画出图形Rt△A1B1C1 , 并写出点A1的坐标;(2)、将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2 , 试在图上画出图形Rt△A2B2C2.并写出顶点A从开始到A2经过的路径长23. 某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)、求A、B型号衣服进价各是多少元?(2)、若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.24. 如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P. (1)、求证:PD是⊙O的切线;(2)、求证:△PBD∽△DCA;(3)、当AB=6,AC=8时,求线段PB的长.25. 甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题:
(1)、求证:PD是⊙O的切线;(2)、求证:△PBD∽△DCA;(3)、当AB=6,AC=8时,求线段PB的长.25. 甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题: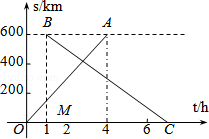 (1)、从图象看,普通快车发车时间比第一列动车组列车发车时间1h(填”早”或”晚”),点B的纵坐标600的实际意义是;(2)、请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象;(3)、若普通快车的速度为100km/h,
(1)、从图象看,普通快车发车时间比第一列动车组列车发车时间1h(填”早”或”晚”),点B的纵坐标600的实际意义是;(2)、请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象;(3)、若普通快车的速度为100km/h,①求第二列动车组列车出发多长时间后与普通快车相遇?
②请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔.
26. 如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.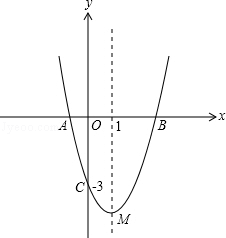 (1)、求抛物线对应的函数表达式;(2)、经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;(4)、当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).
(1)、求抛物线对应的函数表达式;(2)、经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;(4)、当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).