浙江省温州市乐清市2018-2019学年九年级下学期数学3月月考试卷
试卷更新日期:2019-05-23 类型:月考试卷
一、单选题(共10题,共40分)
-
1. tan60°的值等于( )A、1 B、 C、 D、22. 已知⊙O的半径是5cm,点O到同一平面内直线a的距离为4cm,则直线a与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、相交或相离3. 如图,在地面上的点A处测得树顶B的仰角为a,AC=7米,则树高BC为()
 A、7sina米 B、7cosa米 C、7tana米 D、 米4. 某校学生家庭作业完成时间情况的统计图如图所示,若该校作业完成时间在l小时内的学生有300人,则该校作业完成时间在2-3小时的学生有( )
A、7sina米 B、7cosa米 C、7tana米 D、 米4. 某校学生家庭作业完成时间情况的统计图如图所示,若该校作业完成时间在l小时内的学生有300人,则该校作业完成时间在2-3小时的学生有( ) A、200人 B、400人 C、450人 D、550人5. 一元一次不等式3(x+1)≤6的解集在数轴上表示正确的是( )A、
A、200人 B、400人 C、450人 D、550人5. 一元一次不等式3(x+1)≤6的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、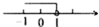 6. 如图,在平面直角坐标系中,OM与x轴相切于点A,与y轴交于B、C两点,M的坐标为(3,5),则B的坐标为( )
6. 如图,在平面直角坐标系中,OM与x轴相切于点A,与y轴交于B、C两点,M的坐标为(3,5),则B的坐标为( )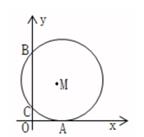 A、(0,5) B、(0,7) C、(0,8) D、(0,9)7. 已知a=2 ,b= ,则a,b的大小关系为( )A、a=b B、a<b C、a>b D、无法比较8. 已知温州至杭州铁路长为380千米,从温州到杭州乘“G”列动车比乘“D”列动车少用20分钟,“G”列动车比“D”列动车每小时多行驶30千米,设“G”列动车速度为每小时x千米,则可列方程为( )A、 B、 C、 D、9. 如图,菱形ABCD中,sin∠BAD= ,对角线AC,BD相交于点O,以O为圆心,OB为半径作⊙O交AD于点E,已知DE=1cm.菱形ABCD的周长为( )
A、(0,5) B、(0,7) C、(0,8) D、(0,9)7. 已知a=2 ,b= ,则a,b的大小关系为( )A、a=b B、a<b C、a>b D、无法比较8. 已知温州至杭州铁路长为380千米,从温州到杭州乘“G”列动车比乘“D”列动车少用20分钟,“G”列动车比“D”列动车每小时多行驶30千米,设“G”列动车速度为每小时x千米,则可列方程为( )A、 B、 C、 D、9. 如图,菱形ABCD中,sin∠BAD= ,对角线AC,BD相交于点O,以O为圆心,OB为半径作⊙O交AD于点E,已知DE=1cm.菱形ABCD的周长为( ) A、4cm B、5cm C、8cm D、10cm10. 如图在Rt△ABC中,∠ACB=90°,AC=6,BC=8,⊙O是△ABC的内切圆,连接AO,BO.则图中阴影部分的面积之和( )
A、4cm B、5cm C、8cm D、10cm10. 如图在Rt△ABC中,∠ACB=90°,AC=6,BC=8,⊙O是△ABC的内切圆,连接AO,BO.则图中阴影部分的面积之和( )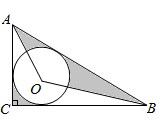
A、 B、 C、12 D、14二、填空题(共6题,共30分)
-
11. 分解因式:x2+xy= .12. 有一组互不相等的数据(每个数都是整数):2,4,6,a,8,它们的中位数是6,则整数a是 .13. 如图,圆锥的底面半径为1 cm,母线AB的长为3 cm,则这个圆锥侧面展开图扇形的圆心角为度.
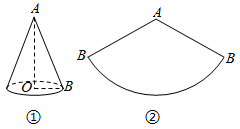 14. 如图,在 ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 的长为.
14. 如图,在 ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 的长为. 15. 直角坐标系中△OAB,△BCD均为等毅直角三角形,OA=AB,BD=CD,点A在x轴的正半轴上。点D在AB上,△OAAB与△BCD的面积之差为3.反比例函数y= 的图象经过点C,则k的值为.
15. 直角坐标系中△OAB,△BCD均为等毅直角三角形,OA=AB,BD=CD,点A在x轴的正半轴上。点D在AB上,△OAAB与△BCD的面积之差为3.反比例函数y= 的图象经过点C,则k的值为. 16. 如图Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,E为⊙O上一点,连结CE,过C作CD⊥CE,交BE于点D,已知 ,AB= ,DE=5,则tan∠ACE= .
16. 如图Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,E为⊙O上一点,连结CE,过C作CD⊥CE,交BE于点D,已知 ,AB= ,DE=5,则tan∠ACE= .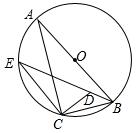
三、解答题(共8题,共80分)
-
17.
(1)、计算; :(2)、先化简,再求值: ,其中x=-2,y= ;18. 已知在△ABC与△ABD中,AC=BD,∠C=∠D=90°,AD与BC交于点E,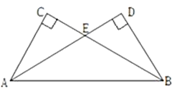 (1)、求证AE=BE;(2)、若AC=3,AB=5,求△ACE的周长.19. 如图是由5个边长为1的正方体叠放而成的一个几何体,请画出这个几何体的三视图.(用铅笔描黑)
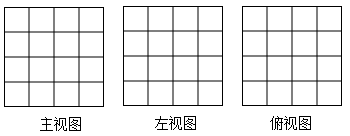
(1)、求证AE=BE;(2)、若AC=3,AB=5,求△ACE的周长.19. 如图是由5个边长为1的正方体叠放而成的一个几何体,请画出这个几何体的三视图.(用铅笔描黑)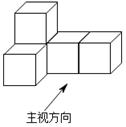
 20. 超速行驶是引发交通事故的主要原因。上周末,小明和三位同学尝试用自己所学的知识检测车速,如图。A0是一条东西方向的路,观测点设在到这条路距离为120米的点P处。这时,一辆小轿车由西向东匀速行使,测得此车从A处行驶到B处所用的时间为5秒且∠APO=60°,∠BPO=45°.
20. 超速行驶是引发交通事故的主要原因。上周末,小明和三位同学尝试用自己所学的知识检测车速,如图。A0是一条东西方向的路,观测点设在到这条路距离为120米的点P处。这时,一辆小轿车由西向东匀速行使,测得此车从A处行驶到B处所用的时间为5秒且∠APO=60°,∠BPO=45°.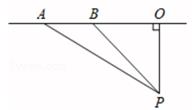 (1)、求A、B之间的路程:(2)、请判断此车是否超过了这条路每小时65千米的限制速度?请说明理由.(参考数据: ≈1.414, ≈1.73).21. 如图,P为⊙O直径AB延长线上的一点,PC切⊙O于点C,过点B作CP的垂线BH交⊙O于点D,交CP于点H,还结AC,CD.
(1)、求A、B之间的路程:(2)、请判断此车是否超过了这条路每小时65千米的限制速度?请说明理由.(参考数据: ≈1.414, ≈1.73).21. 如图,P为⊙O直径AB延长线上的一点,PC切⊙O于点C,过点B作CP的垂线BH交⊙O于点D,交CP于点H,还结AC,CD. (1)、求证:∠PBH=2∠D.(2)、若sin∠P= ,BH=2,求⊙O的半径及BD的长。22. 某灯具厂生产并销售A.B两种型号的智能台灯共100盏,生产并销售一盏A型智能台灯可以获利30元;如果生产并销售不超过20盏B型台灯,则每盏B型台灯可以获利90元,如果超出20盏B型台灯,则每超出1盏,每盏B型台灯获利将均减少2元,设生产并销售B型台灯x盏,(其中x>20)(1)、完成下列表格:
(1)、求证:∠PBH=2∠D.(2)、若sin∠P= ,BH=2,求⊙O的半径及BD的长。22. 某灯具厂生产并销售A.B两种型号的智能台灯共100盏,生产并销售一盏A型智能台灯可以获利30元;如果生产并销售不超过20盏B型台灯,则每盏B型台灯可以获利90元,如果超出20盏B型台灯,则每超出1盏,每盏B型台灯获利将均减少2元,设生产并销售B型台灯x盏,(其中x>20)(1)、完成下列表格:A型
B型
合计
台灯数量(盏)
x
100
每盏台灯获利(元)
30
……..
(2)、当A型台灯所获得的利润比B型台灯所获得利润少200元时,求生产并销售A,B两种台灯各多少盏?(3)、如何设计生产销售方案可以获得最大利润。最大的利润为多少元?23. 已知抛物线y=x2+bx与x轴交于点A,抛物找的对称轴经过点C(2,-2),顶点为M。 (1)、求b的值及直线AC的解析式:(2)、P是抛物线在x轴上方的一个动点,过成P的直线y=-x+m与直线AC交于点D,与直线MC交于点E。连接MD,MP.
(1)、求b的值及直线AC的解析式:(2)、P是抛物线在x轴上方的一个动点,过成P的直线y=-x+m与直线AC交于点D,与直线MC交于点E。连接MD,MP.①当m为何值时,△MDE的面积最大,最大为多少?
②当m为何值时,MP⊥PD?
③DE+DP的最大值是.(直接写出结果)
24. 如图矩形ABCO,点A,C分别在y轴与x轴的正半抽上,O为坐标原点。B的坐标为(6,4),点D(1,0),点P为边AB上一个动点,过点D,P的圆⊙M与AB相切,⊙M交x轴于点E,连接AM. (1)、当P为AB的中点时,求DE的长及⊙M的半径:(2)、当AM⊥DP时,求点P的坐标与⊙M的半径:(3)、是否存在一点P使⊙M与矩形ABCD的另一条边也相切,若存在求出所有符合条件的点P的坐标。
(1)、当P为AB的中点时,求DE的长及⊙M的半径:(2)、当AM⊥DP时,求点P的坐标与⊙M的半径:(3)、是否存在一点P使⊙M与矩形ABCD的另一条边也相切,若存在求出所有符合条件的点P的坐标。