浙江省温州市苍南、永嘉、乐清三县（市）2019年数学初中毕业升生适应性考试

试卷更新日期：2019-05-23 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题4分，共40分。每小题只有一个选项是正确的，不选、多选、错选，均不给分)

1. 给出四个数0， $\sqrt{2}$ ，1，-2，其中最大的数是（）

A、0 B、 $\sqrt{2}$ C、1 D、-2

查看试题解析
2. 有一个正方体原料，挖去一个小正方体，得到如图所示的零件，则这个零件的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 一个不透明的盒子里有3个红球、5个白球，它们除颜色外其他都一样。现从盒子中随机取出一个球，则取出的球是白球的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{5}$ C、 $\frac{5}{8}$ D、 $\frac{3}{8}$

查看试题解析
4. 计算2a²•3a³的结果是（）

A、5a³ B、6a³ C、6a⁶ D、6a⁹

查看试题解析
5. 不等式3（x-2）≥x+4的解集是（）

A、x≥5 B、x≥3 C、x≤5 D、x≥-5

查看试题解析
6. 如图，C，D是⊙O上位于直径AB异侧的两点，若∠ACD=20°，则∠BAD的度数是（）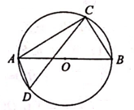

A、40° B、50° C、60° D、70°

查看试题解析
7. 随着电影《流浪地球》的热映，其同名科幻小说的销量也急剧上升．某书店分别用2000元和3000元两次购进该小说，第二次数量比第一次多50套，两次进价相同．设该书店第一次购进x套，根据题意，列方程正确的是（）

A、 $\frac{2000}{x} = \frac{3000}{x - 50}$ B、 $\frac{2000}{x - 50} = \frac{3000}{x}$ C、 $\frac{2000}{x} = \frac{3000}{x + 50}$ D、 $\frac{2000}{x + 50} = \frac{3000}{x}$

查看试题解析
8. 已知反比例函数y=- $\frac{2}{x}$ ，点A(a-b，2），B(a-c，3）在这个函数图象上，下列对于a，b，c的大小判断正确的是（）

A、a<b＜c B、a＜c＜b C、c<b＜a D、b＜c＜a

查看试题解析
9. 如图，直线y=-x+2分别交x轴、y轴于点A，B，点D在BA的延长线上，OD的垂直平分线交线段AB于点C．若△OBC和△OAD的周长相等，则OD的长是（）

A、2 B、2 $\sqrt{2}$ C、 $\frac{5 \sqrt{2}}{2}$ D、4

查看试题解析
10. 在数学拓展课《折叠矩形纸片》上，小林折叠矩形纸片ABCD进行如下操作：①把△ABF翻折，点B落在CD边上的点E处，折痕AF交BC下边于点F；②把△ADH翻折，点D落在AE边上的点G处，折痕AH交CD边于点H．若AD=6，AB=10，则 $\frac{E H}{E F}$ 的值是（）

A、 $\frac{5}{4}$ B、 $\frac{4}{3}$ C、 $\frac{5}{3}$ D、 $\frac{3}{2}$

查看试题解析

二、填空题（本题有6题，每小题5分，共30分）

11. 分解因式：2a²+4a=

查看试题解析
12. 已知函数y= $\sqrt{x + 3}$ ，自变量x的取值范围是．

查看试题解析
13. 若一组数据4，a，7，8，3的平均数是5，则这组数据的中位数是．

查看试题解析
14. AB是半圆O的直径，AB=8，点C为半圈上的一点将此半圆沿BC所在的直线折叠，若配给好过圆心O，则图中阴影部分的面积是．

查看试题解析
15. 图1是一款优雅且稳定的抛物线型落地灯．防滑螺母C为抛物线支架的最高点，灯罩D距离地面1.86米，灯柱AB及支架的相关数据如图2所示。若茶几摆放在灯罩的正下方，则茶几到灯柱的距离AE为米。

查看试题解析
16. 如图，在Rt△ABC中，∠ACB=90°，sin∠BAC= $\frac{2}{3}$ ，点D在AB的延长线上，BD=BC，AE平分∠BAC交CD于点E，若AE=5 $\sqrt{2}$ ，则点A到直线CD的距离AH为， BD的长为．

查看试题解析

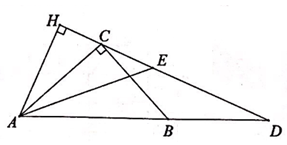
三、解答题（本题有8小题，共80分，解答需写出必要的文字说明、演算步骤或证明过程）

17.

(1)、计算：(-2）²+ $\sqrt{12}$ -（2 $\sqrt{3}$ ）⁰ ．

(2)、化简：（a+2)(a-2)-a（a-4)．

查看试题解析
18. 如图，在▱ABCD中，DE平分∠ADB，交AB于E，A。BF平分∠CBD，交CD于点F．

(1)、求证：△ADB≌△CBF

(2)、当AD与BD满足什么数量关系时，四边形DEBF是矩形？请说明理由。

查看试题解析

19. 某报社为了解温州市民对大范围雾霾天气的成因、影响以及应对措施的看法，做了一次抽样调查，调查结果共分为四个等级：A．非常了解：B．比较了解：C．基本了解；D．不了解．根据调查统计结果，绘制了不完整的三种统计图表．请结合统计图表，回答下列问题：

	对雾霾的了解程度	百分比
A	非常了解	5%
B	比较了解	m%
C	基本了解	45%
D	不了解	n%

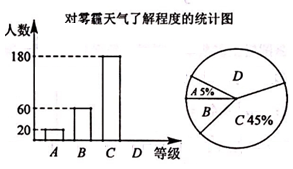(1)、本次参与调查的市民共有人，m= ， n= ．

(2)、统计图中扇形D的圆心角是度。

(3)、某校准备开展关于雾霾的知识竞赛，九（3）班郑老师欲从2名男生和1名女生中任选2人参加比赛，求恰好选中“1男1女”的概率（要求列表或画树状图）．

查看试题解析

20. 在直角坐标系中，我们把横、纵坐标都为整数的点称为整点。如图，已知整A（2，2），B(4，1)，请在所给网格区域(含边界）上找到整点P．

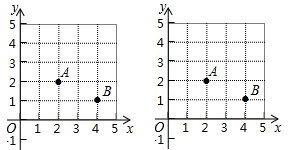(1)、画一个等腰三角形PAB，使点P的纵坐标比点A的横坐标大1．

(2)、若△PAB是直角三角形，则这样的点P共有个.

查看试题解析
21. 如图，点E在△ABC的边AB上，过点B，C，E的⊙O切AC于点C．直径CD交BE于点F，连结BD，DE．已知∠A=∠CDE，AC=2 $\sqrt{2}$ ，BD=1．

(1)、求⊙O的直径。

(2)、过点F作FG⊥CD交BC于点G，求FG的长。

查看试题解析
22. 如图，抛物线y=-x²+4x-1与y轴交于点C，CD∥x轴交抛物线于另一点D，AB∥x轴交抛物线于点A，B，点A在点B的左侧，且两点均在第一象限，BH⊥CD于点H．
设点A的横坐标为m．

(1)、当m=1时，求AB的长。

(2)、若AH= $\sqrt{2}$ （CH-DH），求m的值。

查看试题解析
23. 现有一块矩形地皮，计划共分九个区域区域甲、乙是两个矩形主体建筑，区域丙为梯形停车场，区城①-④是四块三角形绿化区，△AEL和△CIJ为综合办公区（如图所示）．∠HEL=∠ELI=90°，MN//BC．AD=220米，AL=40米，AE=IC=30米．

(1)、求HI的长

(2)、若BG=KD，求主体建筑甲和乙的面积和。

(3)、设LK=3x米，绿化区②的面积为S平方米。若要求绿化区②与④的面积之差不少于1200平方米，求S关于x的函数表达式。并求出S的最小值

查看试题解析
24. 如图，AB是半圈O的直径，率径OC⊥AB，OB=4，D是OB的中点，点E是BC上一动点，连结AE，DE．

(1)、当点E是BC的中点时，求△ADE的面积

(2)、若tan∠AED= $\frac{3}{2}$ ，求AE的长，

(3)、点F是半径OC上一动点，设点E到直线OC的距离为m。
①当△DEF是等腰直角三角形时，求m的值．

②延长DF交半圆弧于点G，若AG=EG，AG∥DE，直接写出DE的长。

查看试题解析