浙江省湖州市2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2019-05-23 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，共30分）

1. 要使二次根式 $\sqrt{x + 2}$ 有意义，则x的取值范围是（）

A、x＞-2 B、x≥-2 C、x≠-2 D、x≤-2

查看试题解析
2. 下面计算正确的是（）

A、 $\sqrt{5^{2}} = \pm 5$ B、 $\sqrt{8} \div \sqrt{2} = 4$ C、 ${(- \sqrt{5})}^{2} =- 5$ D、 $3 \sqrt{5} - \sqrt{5} = 2 \sqrt{5}$

查看试题解析
3. 下列方程中是一元二次方程的是（）

A、2x+1=0 B、x²+y=1 C、x²+2=0 D、 $\frac{1}{x} + x^{2} = 1$

查看试题解析
4. 以下是回收、绿色包装、节水、低碳四个标志，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 若数据2，x，4，8的平均数是4，则这组数据的中位数和众数是（　　）

A、2和3 B、3和2 C、2和2 D、2和4

查看试题解析
6. 在四边形ABCD中，对角线AC与BD交于点O，下列条件不能判定这个四边形是平行四边形的是（）

A、OA=OC，OB=OD B、AD∥BC，AB∥DC C、AB=DC，AD=BC D、AB∥DC，AD=BC

查看试题解析
7. 要使关于x的方程ax²+3x+4=0有两个不相等的实数根，则a的取值是（）

A、a＜ $\frac{9}{16}$ B、a≤ $\frac{9}{16}$ 且a≠0 C、a＜ $\frac{9}{16}$ 且a≠0 D、a＞ $\frac{9}{16}$

查看试题解析
8. 在国家宏观调控下，某市的商品房成交价由今年1月份的25000元/m²下降到3 月份的20250元/m² ，设平均每月的降价率为x，则下面所列方程中正确的是（）

A、25000(1-2x)=20250 B、25000(1-x)²=20250 C、20250(1-2x)=25000 D、20250(1-x)²=25000

查看试题解析
9. 观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗星，图形③中共有11颗星，图形④中共有17颗星，按此规律，图形⑧中星星的颗数是（）

A、43 B、45 C、51 D、53

查看试题解析
10. 已知点D与点 A(8，0)，B（0，6），C（a，-a）是一平行四边形的四个顶点，则CD长的最小值为（）

A、8 B、7 $\sqrt{2}$ C、6

查看试题解析

二、填空题（本题有6小题，共24分）

11. 八边形的内角和为；外角和为.

查看试题解析
12. 数据-1，0，2，3，1的方差是，标准差是.

查看试题解析
13. 已知 x+ $|x - 1|$ =1 ，则化简 $\sqrt{{(x - 1)}^{2}} + \sqrt{{(2 - x)}^{2}}$ 的结果是.

查看试题解析
14. 已知等腰三角形的一边长为4，它的其他两条边长恰好是关于x的一元二次方程 $x^{2} - 6 x + m = 0$ 的两个实数根，则m的值 .

查看试题解析
15. 对于平面直角坐标系xOy中的点P，给出如下定义：记点P到x轴的距离为d₁ ，到y轴的距离为d₂ ，若 d1≥d₂ ，则称d₁为点P的最大距离；若 d₁＜d₂ ，则称 d₂为点P的最大距离.例如：点P（ -3 ， 4 ）到到x轴的距离为4，到y轴的距离为3，因为3 < 4，所以点P的最大距离为 4 .若点C在直线 y=-x-2 上，且点C的最大距离为 5 ，则点C的坐标是.

查看试题解析
16. 如图，在 ▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，①∠DCF= $\frac{1}{2}$ ∠BCD；②EF=CF； ③S_△BEC=2S_△CEF；④∠DFE=3∠AEF．则结论一定成立的是.

查看试题解析

三、解答题(本题有8小题，共66分，各小题都必须写出解答过程)

17. 解方程：

(1)、(x-1)²=16

(2)、4x²-7x+1=0

查看试题解析
18. 计算：

(1)、 $\sqrt{8} - \sqrt{2} \times {(1 - \sqrt{2})}^{0}$

(2)、 $\sqrt{12} + \sqrt{\frac{1}{3}} + \sqrt{{(\sqrt{3} - 2)}^{2}}$

查看试题解析
19. 如图，已知BD为▱ABCD的对角线，O为BD的中点，EF⊥BD于点O，与AD，BC分别交于点E，F。求证：DE=DF.

查看试题解析
20. 关于x的方程x²﹣2x+k﹣1=0有两个不相等的实数根。

(1)、求k的取值范围.

(2)、若k﹣1是方程x²﹣2x+k﹣1=0的一个根，求k的值．

查看试题解析
21. 某初级中学数学兴趣小组为了了解本校学生的年龄情况，随机调查了该校部分学生的年龄，整理数据并绘制如下不完整的统计图．依据以上信息解答以下问题：

(1)、求样本容量；

(2)、直接写出样本容量的平均数，众数和中位数；

(3)、若该校一共有1800名学生，估计该校年龄在15岁及以上的学生人数．

查看试题解析
22. 如图，M、N是平行四边形ABCD对角线BD上两点．

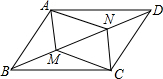
(1)、若BM=MN=DN，求证：四边形AMCN为平行四边形；

(2)、若M、N为对角线BD上的动点（均可与端点重合），设BD=12cm，点M由点B向点D匀速运动，速度为2（cm/s），同时点N由点D向点B匀速运动，速度为a（cm/s），运动时间为t（s）．若要使四边形AMCN为平行四边形，求a的值及t的取值范围．

查看试题解析
23. 某市场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元.为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当降价措施.经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件.求：

(1)、若商场平均每天赢利1200元，且让顾客得到实惠，每件衬衫应降价多少元？

(2)、要使商场平均每天赢利最多，请你帮助设计方案.

查看试题解析
24. 在平面直角坐标系xOy中，O为坐标原点，四边形OABC的顶点A在 $°$ 轴的正半轴上，OA=4，OC=2，点P，点Q分别是边BC，边AB上的点，连结AC，PQ，点B₁是点B关于PQ的对称点.

(1)、若四边形OABC为长方形，如图1，
①求点B的坐标；
②若BQ=BP，且点B₁落在AC上，求点B₁的坐标；

(2)、若四边形OABC为平行四边形，如图2，且OC⊥AC，过点B₁作B₁F∥ x 轴，与对角线AC，边OC分别交于点E，点F.若B₁E： B₁F=1：3，点B₁的横坐标为m，求点B₁的纵坐标（用含m的代数式表示）.

查看试题解析