浙江省台州市天台县2019年中考适应性检测九年级数学试卷
试卷更新日期:2019-05-23 类型:中考模拟
一、选择题(本题有l0小题,每小题3分,共30分)
-
1. 下列选项中的实数,属于无理数的是( )A、-2 B、 C、 D、2. 根据省统计局统一核算,2018年某市实现地区生产总值271900000000元.将271900000000用科学记数法表示为( )A、2.719×109 B、2.719x1010 C、2.719×1011 D、2.719×10123. 下面四个几何体中,其主视图不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、m3+m3=m6 B、m3 ▪ m2=m6 C、(m3)2=m5 D、m3÷m2=m5. -个布袋里装有3个红球,2个白球,每个球除颜色外均相同,从中任意摸出-个球,则摸出的球是红球的概率是( )
4. 下列计算正确的是( )A、m3+m3=m6 B、m3 ▪ m2=m6 C、(m3)2=m5 D、m3÷m2=m5. -个布袋里装有3个红球,2个白球,每个球除颜色外均相同,从中任意摸出-个球,则摸出的球是红球的概率是( )
A、 B、 C、 D、6. 过△ABC的重心G作GE∥BC交AC于点E,线段BC=12,线段GE长为( )A、4 B、4.5 C、6 D、87. 若-个圆锥的侧面展开图是半径为lOcm,圆心角为120°的扇形,则该圆锥的底面半径是( )A、 cm B、 cm C、 cm D、 cm8. 如图,在平面直角坐标系中, ABOC的顶点B,C在反比例函数y= (x>O)的图象上,点A在反比例函数y= (k>O)的图象上,若点B的坐标为(1,2),∠OBC=90°,则k的值为( )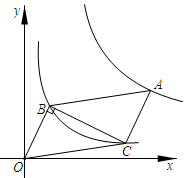 A、 B、3 C、5 D、9. 如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0 (t为实数)在1<x<3的范围内有解,则t的取值范围是( )
A、 B、3 C、5 D、9. 如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0 (t为实数)在1<x<3的范围内有解,则t的取值范围是( ) A、-5<t≤4 B、3<t≤4 C、-5<t<3 D、t>-510. 如图,在平面直角坐标系中有-个3×3的正方形网格,其左下角格点A的坐标为(1,1),右上角格点B的坐标为(4,4),若分布在直线y=k(x-1)两侧的格点数相同,则k的取值可以是( )
A、-5<t≤4 B、3<t≤4 C、-5<t<3 D、t>-510. 如图,在平面直角坐标系中有-个3×3的正方形网格,其左下角格点A的坐标为(1,1),右上角格点B的坐标为(4,4),若分布在直线y=k(x-1)两侧的格点数相同,则k的取值可以是( )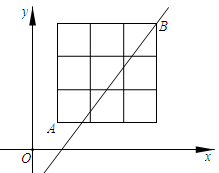 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. -2的倒数等于.12. 因式分解:a3-4a= .13. 若m2-3m+1=0,则2-m- 的值为 .14. 某建筑物的走廊墙壁上搭了-个长4m的梯子,梯子底端正好与地面成45°角,影响了人们的正常行走.为了拓宽行路通道,将梯子挪动位置,使其与地面的倾斜角恰为60°,则行路通道被拓宽了m(结果保留根号).15. 如图,正方形ABCD的边长为4cm,点E,F分别是BC,CD的中点,连结BF,DE,则图中阴影部分的面积是cm2.
 16. 如图,在平面直角坐标系中,△ABC的顶点在坐标轴上,A,B,C三点的坐标分别为 (0,2),(1,0),(0,-0.5),D为线段AB上-个动点(不与点A,B重合),过B,D,0三点的圆与直线BC交于点E,当△OED面积取得最小值时,ED的长为 .
16. 如图,在平面直角坐标系中,△ABC的顶点在坐标轴上,A,B,C三点的坐标分别为 (0,2),(1,0),(0,-0.5),D为线段AB上-个动点(不与点A,B重合),过B,D,0三点的圆与直线BC交于点E,当△OED面积取得最小值时,ED的长为 .
三、解答题(本题有8小题,共66分)
-
17. 化简:(a+1)2-2a(a-1).18. 解方程组:19. 如图,已知△ABC是等边三角形,以AC为斜边作Rt△ADC,∠ADC=90°,且AD∥BC,连结BD交AC于点E.
 (1)、求证:BC=2AD.(2)、若BC=4,求BE的长.20. 居民区内的“广场舞”引起媒体关注,小王想要了解本小区居民对“广场舞”的看法,于是进行了-次抽样调查,把居民对“广场舞”的看法分为四类:
(1)、求证:BC=2AD.(2)、若BC=4,求BE的长.20. 居民区内的“广场舞”引起媒体关注,小王想要了解本小区居民对“广场舞”的看法,于是进行了-次抽样调查,把居民对“广场舞”的看法分为四类:
A.非常赞同; B.赞同但要有时间限制; C.无所谓; D.不赞同.
并将调查结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
 (1)、①本次被抽查的居民人数是人;将条形统计图补充完整.
(1)、①本次被抽查的居民人数是人;将条形统计图补充完整.②图l中∠ 的度数是度;该小区有3000名居民,请估计对“广场舞”表示赞同(包括A类和B类)的大约有人.
(2)、小王想从甲,乙,丙,丁四位居民中随机选取两位了解具体情况,请用列表或画树状图的方法求出恰好同时选中甲和乙两位居民的概率.21. 如图,已知,⊙O的半径OC垂直于弦AB,垂足为点D,点P在OC的延长线上,连结AP,AC平分∠PAB. (1)、求证:PA是⊙O的切线;(2)、若sinP= ,AB=16,求⊙O的半径长.22. 为建设美丽家园,某社区将辖区内的-块面积为1000m2的空地进行绿化,-部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用yl(元)与x(m2)的函数关系图象如图所示,栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.Olx2-20x+30000(0≤x≤1000).
(1)、求证:PA是⊙O的切线;(2)、若sinP= ,AB=16,求⊙O的半径长.22. 为建设美丽家园,某社区将辖区内的-块面积为1000m2的空地进行绿化,-部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用yl(元)与x(m2)的函数关系图象如图所示,栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.Olx2-20x+30000(0≤x≤1000). (1)、求yl(元)与x(m2)的函数关系式;(2)、设这块1000m2空地的绿化总费用为W(元),请利用W与x的函数关系式,求绿化总费用W的最大值.23. 如图
(1)、求yl(元)与x(m2)的函数关系式;(2)、设这块1000m2空地的绿化总费用为W(元),请利用W与x的函数关系式,求绿化总费用W的最大值.23. 如图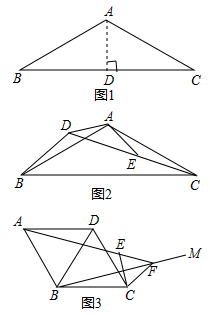 (1)、【问题背景】如图1,等腰△ABC,AB=AC,∠BAC=120°则 = .(2)、【迁移应用】如图2,△ABC和△ABE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同-条直线上,连结BD.求线段AD,BD,CD之间的数量关系式;(3)、【拓展延伸】如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连结AE并延长交BM于点F,连结CE, CF.若AE=4,CE=1.求BF的长.24. 如图,在平面直角坐标系中,直线y=-2x+2与x轴交于点B,与y轴交于点A,抛物线y=- x2+bx+c与线段AB交于点E,并经过原点O,且点E的横坐标为 .
(1)、【问题背景】如图1,等腰△ABC,AB=AC,∠BAC=120°则 = .(2)、【迁移应用】如图2,△ABC和△ABE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同-条直线上,连结BD.求线段AD,BD,CD之间的数量关系式;(3)、【拓展延伸】如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连结AE并延长交BM于点F,连结CE, CF.若AE=4,CE=1.求BF的长.24. 如图,在平面直角坐标系中,直线y=-2x+2与x轴交于点B,与y轴交于点A,抛物线y=- x2+bx+c与线段AB交于点E,并经过原点O,且点E的横坐标为 .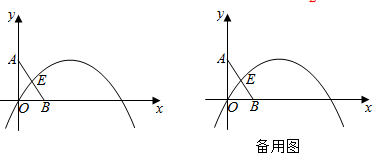 (1)、求抛物线的表达式;(2)、在抛物线上是否存在点C,使得以AC为直径的圆恰好经过点B,若存在,求出所有满足条件的点C的坐标,若不存在,请说明理由;(3)、若D是第(2)小题中圆上的动点,直线y= x+m经过点D,求m的取值范围.
(1)、求抛物线的表达式;(2)、在抛物线上是否存在点C,使得以AC为直径的圆恰好经过点B,若存在,求出所有满足条件的点C的坐标,若不存在,请说明理由;(3)、若D是第(2)小题中圆上的动点,直线y= x+m经过点D,求m的取值范围.