浙江省宁波市海曙区2019年初中毕业生学业模拟考试数学试卷
试卷更新日期:2019-05-23 类型:中考模拟
一、选择题(每小题4分,共48分,)
-
1. 在 , ,3,-4这四个实数中,最大的数是( )A、 B、 C、3 D、-42. 下列算式中,计算结果为a5的是( )A、a2▪a3 B、(a2)3 C、a2+a3 D、a4÷a3. 某课题小组针对200吨垃圾再利用的情况进行了调查并绘制了如下不完整的条形统计图和扇形统计图,则条形统计图中a的值为( )
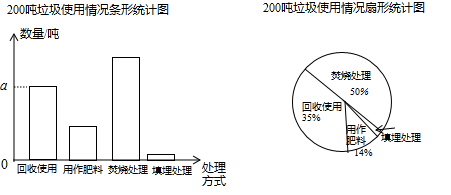 A、100吨 B、70吨 C、28吨 D、2吨4. 将某个图形的各个顶点的横坐标都减去2,纵坐标保持不变,可将该图形( )A、向左平移2个单位 B、向右平移2个单位 C、向上平移2个单位 D、向下平移2个单位5. 若一个多边形的内角和为720°,则这个多边形的边数为( )A、4 B、5 C、 6 D、 76. 已知反比例函数y= 在其各个分支上y随x的增大而减小,则m的取值范围是( )A、m>1 B、m<1 C、m>O D、m<O7. 下列说法中,正确的是( )A、一个游戏中奖的概率是 ,则做10次这样的游戏一定会中奖 B、为了了解一批炮弹的杀伤半径,应采用全面调查的方式 C、一组数据8,8,7,10,6,8,9的众数是8 D、一组数据的方差越大说明这组数据的波动越小8. 若一次函数y=kx+b的图象位置如图所示,则k,b的取值范围是( )
A、100吨 B、70吨 C、28吨 D、2吨4. 将某个图形的各个顶点的横坐标都减去2,纵坐标保持不变,可将该图形( )A、向左平移2个单位 B、向右平移2个单位 C、向上平移2个单位 D、向下平移2个单位5. 若一个多边形的内角和为720°,则这个多边形的边数为( )A、4 B、5 C、 6 D、 76. 已知反比例函数y= 在其各个分支上y随x的增大而减小,则m的取值范围是( )A、m>1 B、m<1 C、m>O D、m<O7. 下列说法中,正确的是( )A、一个游戏中奖的概率是 ,则做10次这样的游戏一定会中奖 B、为了了解一批炮弹的杀伤半径,应采用全面调查的方式 C、一组数据8,8,7,10,6,8,9的众数是8 D、一组数据的方差越大说明这组数据的波动越小8. 若一次函数y=kx+b的图象位置如图所示,则k,b的取值范围是( )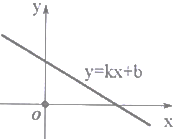 A、k>0,b>O B、k>0,b<0 C、k<0,b<0 D、k<0,b>O9. 已知钝角△ABC中,∠A=30°,则下列结论正确的是( )A、0°<∠B<60° B、90°<∠B<150° C、0°<∠B<60°或90°<∠B<150° D、以上都不对10. 如图,在矩形ABCD中放入6个全等的小矩形,所标尺寸如图所示,设小矩形的长为a,宽为b,则可得方程组( )
A、k>0,b>O B、k>0,b<0 C、k<0,b<0 D、k<0,b>O9. 已知钝角△ABC中,∠A=30°,则下列结论正确的是( )A、0°<∠B<60° B、90°<∠B<150° C、0°<∠B<60°或90°<∠B<150° D、以上都不对10. 如图,在矩形ABCD中放入6个全等的小矩形,所标尺寸如图所示,设小矩形的长为a,宽为b,则可得方程组( )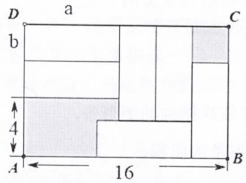 A、 B、 C、 D、11. 在玩俄罗斯方块游戏时,底部已有的图形如图所示,接下去出现如下哪个形状时,通过旋转变换后能与已有图形拼成一个中心对称图形( )
A、 B、 C、 D、11. 在玩俄罗斯方块游戏时,底部已有的图形如图所示,接下去出现如下哪个形状时,通过旋转变换后能与已有图形拼成一个中心对称图形( )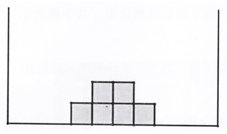 A、
A、 B、
B、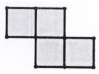 C、
C、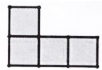 D、
D、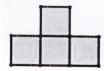 12. 如图,点C的坐标为(3,4),CA⊥y轴于点A,D是线段AO上一点,且OD=3AD,点B从原点O出发,沿x轴正方向运动,CB与直线y= x交于点E,则△CDE的面积( )
12. 如图,点C的坐标为(3,4),CA⊥y轴于点A,D是线段AO上一点,且OD=3AD,点B从原点O出发,沿x轴正方向运动,CB与直线y= x交于点E,则△CDE的面积( )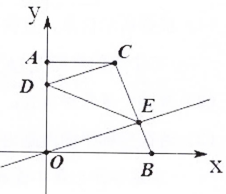 A、逐渐变大 B、先变大后变小 C、逐渐变小 D、始终不变
A、逐渐变大 B、先变大后变小 C、逐渐变小 D、始终不变二、填空题(每小题4分,共24分)
-
13. 二次根式 有意义,则x的取值范围是 .14. 若 ,则a+b= .15. 一个空间几何体的主视图和左视图都是边长为2cm的正三角形,俯视图是一个圆,那么这个几何体的侧面积是cm2 .16. 如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G.若CD⊥AC,EF=9,EG=4,则AC的长为 .
 17. 已知自变量为x的二次函数y=(ax+b)(x+ )经过(m,3)、(m+4,3)两点,若方程(ax+b)(x+ )=0的一个根为x=5,则其另一个根为 .18. 已知点C为函数y= (x>0)上一点,过点C平行于x轴的直线交y轴于点D,交函数y= 于点A,作AB⊥CO于E,交y轴于B,若∠BCA=45°,△OBC的面积为l4,则m= .
17. 已知自变量为x的二次函数y=(ax+b)(x+ )经过(m,3)、(m+4,3)两点,若方程(ax+b)(x+ )=0的一个根为x=5,则其另一个根为 .18. 已知点C为函数y= (x>0)上一点,过点C平行于x轴的直线交y轴于点D,交函数y= 于点A,作AB⊥CO于E,交y轴于B,若∠BCA=45°,△OBC的面积为l4,则m= .
三、解答题(第19题6分,第20、21题每题8分,第22、23、24题每题10分,第25题12分,第26题14分,共78分)
-
19. 化简:20. 如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA= .
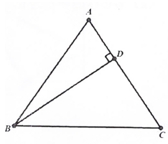 (1)、求BD的长.(2)、求tanC的值.21. 在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形。小明有一副三角尺和一个量角器(如图所示)
(1)、求BD的长.(2)、求tanC的值.21. 在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形。小明有一副三角尺和一个量角器(如图所示)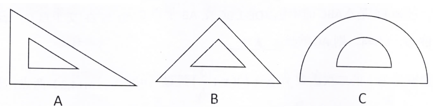 (1)、小明在这三件文具中任取一件,结果是轴对称图形的概率是;(2)、小明把A、B两把尺的各任意一个角拼在一起(无重叠无缝隙)得到一个更大的角,请画树状图或列表说明这个角是钝角的概率是多少.22. 某写字楼门口安装了一个如图所示的旋转门,旋转门每转一圈按正常负载可以出去6人,每分钟转4圈。
(1)、小明在这三件文具中任取一件,结果是轴对称图形的概率是;(2)、小明把A、B两把尺的各任意一个角拼在一起(无重叠无缝隙)得到一个更大的角,请画树状图或列表说明这个角是钝角的概率是多少.22. 某写字楼门口安装了一个如图所示的旋转门,旋转门每转一圈按正常负载可以出去6人,每分钟转4圈。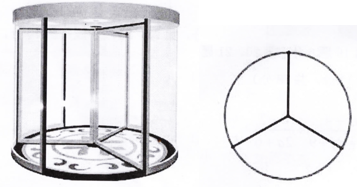 (1)、问:按正常负载半小时此旋转门可出去多少人;(2)、紧急情况时,旋转门每圈负载出去人数可增加50%,但因此每分钟门的转速降低25%,
(1)、问:按正常负载半小时此旋转门可出去多少人;(2)、紧急情况时,旋转门每圈负载出去人数可增加50%,但因此每分钟门的转速降低25%,①直接写出紧急情况时旋转门每分钟可以出去人;
②该写字楼有9层,每层10间办公室,平均每个办公室6人。为了符合消防安全要求,要在一楼再安装几道普通侧门,每道侧门每分钟能通过45人。在紧急情况下,要使整幢写字楼的人能在5分钟内全部安全撤离(下楼时间忽略不计),至少要安装几道普通侧门.
23. 如图,AB是⊙O的直径,AC是⊙O的切线,过点B作BD∥OC交⊙O于点D. (1)、求证:CD是⊙O的切线;
(1)、求证:CD是⊙O的切线;
(2)、若⊙O的半径为6,∠B=60°,求图中阴影部分的面积.24. 在坐标平面内,以x轴上的1个单位长为底边按一定规律向上画矩形条。现已知其中几个矩形条的位置如图,其相应信息如下表单位底位置
...
-3~-2
-2~-l
-l~0
0~1
1~2
2~3
3~4
...
矩形条高
…
1
...
...
3.5
...
...
15
...
看所有矩形条的左上顶点都在同一个我们已学的某类函数图象上。
 (1)、根据所给信息,直接写出这个函数图象上的三个点的坐标 .(2)、求这个函数解析式;(3)、若在坐标平面内画出所有这样依次排列的矩形条,求这些矩形条中面积最小矩形条的面积.25. 若矩形的内接平行四边形的一组邻边分别与矩形的两条对角线平行,这样的平行四边形叫做这个矩形的台球四边形。
(1)、根据所给信息,直接写出这个函数图象上的三个点的坐标 .(2)、求这个函数解析式;(3)、若在坐标平面内画出所有这样依次排列的矩形条,求这些矩形条中面积最小矩形条的面积.25. 若矩形的内接平行四边形的一组邻边分别与矩形的两条对角线平行,这样的平行四边形叫做这个矩形的台球四边形。 (1)、如图l,四边形EFGH是矩形ABCD的台球四边形,AC、BD.交于点0。求证:∠1=∠2(2)、小明尝试借用作图对台球四边形的性质进行探究:
(1)、如图l,四边形EFGH是矩形ABCD的台球四边形,AC、BD.交于点0。求证:∠1=∠2(2)、小明尝试借用作图对台球四边形的性质进行探究:①在图2、图3的正方形网格中,请你仅用直尺作出矩形ABCD的台球四边形(其中格点E为台球四边形的一个顶点)
②借助图形,小明进一步探究台球四边形的性质,得到了如下两个猜想,请你判断(对的打√,错的打×).
a.一个矩形的台球四边形的周长等于这个矩形两条对角线的和()
b.一个矩形的台球四边形的面积不超过这个矩形面积的一半()
(3)、如图4,四边形EFGH是矩形ABCD的台球四边形,若AD=4,AB=8,EG⊥HG,求AE的长.26. 如图l,已知⊙M与x轴交于A,B两点,与y轴交于C、D两点,A、B两点的横坐标分别为一1和7,弦AB的弦心距MN为3,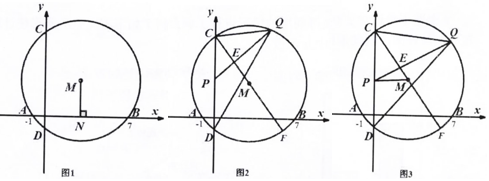 (1)、求⊙M的半径:(2)、如图2,P在弦CD上,且CP=2,Q是 上一动点,PQ交直径CF于点E,当∠CPQ=∠CQD时,
(1)、求⊙M的半径:(2)、如图2,P在弦CD上,且CP=2,Q是 上一动点,PQ交直径CF于点E,当∠CPQ=∠CQD时,①判断线段PQ与直径CF的位置关系,并说明理由;
②求CQ的长;
(3)、如图3,若P点是弦CD上一动点,Q是 上一动点,PQ交直径CF于点E,当∠CPQ与∠CQD互余时,求△PEM面积的最大值.