浙江省宁波市余姚市2019届九年级下学期初中学业水平测试数学试卷

试卷更新日期：2019-05-23 类型：水平会考

进入出卷网下载

一、选择题(每小题4分．共48分．)

1. 在-4，-2.5, 0，1四个数中，比-3小的数是（）

A、-4 B、-2.5 C、0 D、1

查看试题解析
2. 4月上旬，宁波市统计局组织开展了2019年一季度交通出行公众满意度调查，采集样本1889个，其中“1889”用科学记数法表示为（）

A、0.1889×10⁴ B、0.1889×10³ C、1.889×10⁴ D、1.889×10³

查看试题解析
3. 下列计算正确的是（）

A、x＋x²＝x³ B、2x－3x＝－x C、(x²)³＝x⁵ D、x⁶÷x³＝x²

查看试题解析
4. 袋中有五个小球，3个红球，2个白球，它们除了颜色外其余完全一样．现从中任意摸一个球．摸出红球的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
5. 下列图形中，是圆锥的侧面展开图的为（）

A、 B、 C、 D、

查看试题解析
6. 能说明命题“若|a|=|b|，则a=b”是假命题的反例为（）

A、a=2,b=-2 B、a=1,b=0 C、a=1,b=1 D、a=-3,b= $\frac{1}{3}$

查看试题解析
7. 红领巾的形状是等腰三角形，底边长为100厘米，腰长为60厘米，则底角（）

A、小于30° B、大于30°且小于45° C、等于30° D、大于45°且小于60°

查看试题解析
8. 下图是方程 $\frac{x - 1}{2} + 1 = \frac{2 x + 1}{3}$ 的变形求解过程，其中“去括号”的步骤是（）

A、① B、② C、③ D、④

查看试题解析
9. 如图，在△ABC中，∠ABC=70°，按如下步骤作图：
第一步，以点A为圆心，BC长为半径作弧．再以点C为圆心，AB长为半径作弧，两弧的交点记为D，连结AD，CD；
第二步，以点D为圆心，CD长为半径作弧，交AD于点E，连结CE．则∠BCE的度数为（）

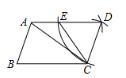A、55° B、60° C、65° D、70°

查看试题解析
10. 如图，在Rt△ABC中，∠ACB=90°，DE是△ABC的中位线，连结CD．下列各组线段的比值一定与cosA相等的是（）

A、 $\frac{D E}{A D}$ B、 $\frac{D E}{A E}$ C、 $\frac{C E}{B D}$ D、 $\frac{C E}{B C}$

查看试题解析
11. 如图，⊙O与矩形ABCD的边AB，CD，AD相切，切点分别为E，F，G，边BC与⊙O交于M，N两点．下列五组条件中，能求出⊙O半径的有①已知AB，MN的长；②已知AB，BM的长；③已知AB，BN的长；④已知BE，BN的长；⑤已知BM，BN的长．（）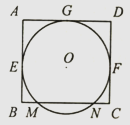

A、2组 B、3组 C、4组 D、5组

查看试题解析
12. 如图，四张大小不一的正方形纸片分别放置于矩形的四个角落，其中，①和②纸片既不重叠也无空隙．在矩形ABCD的周长已知的情况下，知道下列哪个正方形的边长，就可以求得阴影部分的周长（）

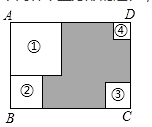A、① B、② C、③ D、④

查看试题解析

二、填空题(每小题4分．共24分)

13. 因式分解：2x²-8= ．

查看试题解析
14. 若二次根式 $\sqrt{2 x - 3}$ 有意义，则x的取值范围是．

查看试题解析
15. 平面直角坐标系中，点P(-2，1)绕点O(0，0)顺时针旋转90°后，点P的对应点将落在第象限．

查看试题解析

16. 下图是某小组美术作业得分情况，则该小组美术作业得分的众数为分．

编号	1	2	3	4	5	6	7	8	9	10
得分(分)	3	4	3	5	5	4	3	5	5	4

查看试题解析

17. 直线y=ax+m和直线y=bx+n在同一平面直角坐标系中的图象如图所示，则抛物线y=ax²+bx+c的对称轴为．

查看试题解析
18. 如图，反比例函数y= $\frac{5}{x}$ (x>0)的图象与矩形OABC的边BC交于点D，过点A，D作DE∥AF，交直线y=kx(x<0)于点E，F．若0E=OF，BD= $\sqrt{2}$ CD，则四边形ADEF的面积为．

查看试题解析

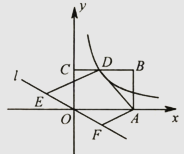
三、解答题(本大题有8小题, 共78分)

19. 解分式方程： $\frac{3}{x^{2} - 9} + \frac{x}{x + 3}$ =1

查看试题解析
20. 6×6的方格图中，按要求作格点三角形ABC．

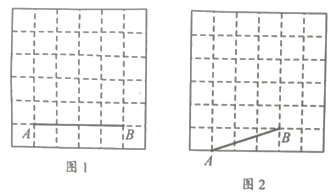(1)、在图1中，作等腰直角△MABC，使得∠BAC=45°；(画出一个即可)

(2)、在图2中，作钝角△ABC，使得∠BAC=45°．

查看试题解析
21. 随着生活水平的日益提高，人们越来越喜欢过节，节日的仪式感日渐浓烈．某校举行了“女神节暖心特别行动”，从中随机调查了部分同学的暖心行动，并将其分为A， B，C，D四种类型(分别对应送服务、送鲜花、送红包、送话语)．现根据调查的数据绘制成如下的条形统计图和扇形统计图．
请根据以上不完整的统计图提供的信息，解答下列问题：

(1)、该校共抽查了多少名同学的暖心行动?

(2)、补全条形统计图和扇形统计图：

(3)、若该校共有2400名同学，请估计该校进行送鲜花行动的同学约有多少名?

查看试题解析
22. 随着科技的发展，智能产品越来越受到人们的喜爱．为了奖励员工，某公司打算采购一批智能音箱．现有A，B两款智能音箱可供选择，已知A款音箱的单价比B款音箱的单价高50元，购买5个A款音箱和4个B款音箱共需1600元．

(1)、分别求出A款音箱和B款音箱的单价：

(2)、公司打算采购A，B两款音箱共20个，且采购A，B两款音箱的总费用不超过3500元，那么A款音箱最多采购多少个?

查看试题解析
23. 如图，在Rt△ABC中，CD是斜边AB上的中线，以CD为直径作⊙O，交BC于点E，过E作EF⊥AB，垂足为F．

(1)、求证：直线EF与⊙O相切；

(2)、若CE=2，EF=1，求 $\overset{⌢}{D E}$ 的长．

查看试题解析
24. 如图，平面直角坐标系中，A(5，0)，B(2，3)，连结OB和AB，抛物线y=-x²+bx经过点A．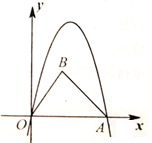

(1)、求b的值和直线AB的解析式；

(2)、若P为抛物线上位于第一象限的一个动点，过p作x轴的垂线，交折线段0BA于Q．当点Q在线段AB上时，求PQ的最大值．

查看试题解析
25. 我们把两边之比为整数的三角形称为倍比三角形．其中，这个整数比称为倍比．第三条边叫做该三角形的底．

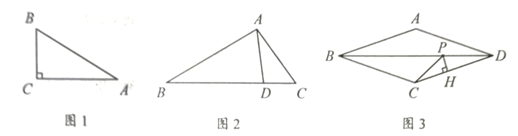(1)、如图1，△ABC是以AC为底的倍比三角形，倍比为3，若∠C=90°，AC= $2 \sqrt{2}$ ，
求BC的长.

(2)、如图2，△ABC中，D为BC边上一点，BD=3．CD=1，连结AD．若AC=2，
求证：△ABD是倍比三角形，并求出倍比；

(3)、如图3，菱形ABCD中，∠BAD为钝角，P为对角线BD上一动点，过P作PH⊥CD于H. 当CP+PH的值最小时，△PCD恰好是以PD为底的倍比三角形，记倍比为x， $\frac{C P}{P H} = y$ ，求y关于x的函数关系式．

查看试题解析
26. 如图1，在矩形ABCD中．点E以1cm／s的速度从点A向点D运动，运动时间为t(s)．连结BE，过点E作EF⊥BE，交CD于F，以EF为直径作⊙O ．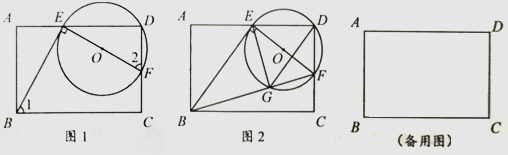

(1)、求证：∠1=∠2；

(2)、如图2，连结BF，交⊙O于点G，并连结EG．已知AB=4，AD=6．
①用含t的代数式表示DF的长；

②连结DG．若△EGD是以EG为腰的等腰三角形。求t的值．

(3)、连结OC ，当tan∠BFC=3时，恰有OC∥EG，请直接写出tan∠ABE的值．

查看试题解析