浙江省宁波市江北区2019届九年级下学期数学学业质量检测试卷

试卷更新日期：2019-05-23 类型：中考模拟

进入出卷网下载

一、选择题(每小题4分，共48分)

1. 在下列实数中，无理数是（）

A、0 B、 $\sqrt{2}$ C、 $\frac{1}{2}$ D、-9

查看试题解析
2. 截止2019年3月8日，中国科幻电影《流浪地球》的票房约为45.6亿元，成为中国科幻电影的里程碑．其中45.6亿用科学记数法表示为（）

A、4.56x10⁸ B、45.6x10⁸ C、4.56x10⁹ D、0.456x10¹⁰

查看试题解析
3. 下列计算正确的是（）

A、x²·x³=x⁵ B、x⁶÷x²=x³ C、x³+x³=x⁶ D、2x-x=2

查看试题解析
4. 如图所示是一个正四棱台，其俯视图正确的为（）

A、 B、 C、 D、

查看试题解析
5. 从五个数-1，0， $\frac{5}{2}$ ， $π$ ，-1.5中任意抽取一个作为x，则满足不等式2x-1≥3的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
6. 将一副三角板如图放置，其中∠BAC=∠ADE=90°，∠E=30°，∠B=45°，其中点D落在线段BC上，且AE∥BC，则∠DAC的度数为（）

A、30° B、25° C、20° D、15°

查看试题解析
7. 一元二次方程x²+6x-7=0的解为（）

A、x₁=1，x₂=7 B、x₁=-1，x₂=7 C、x₁=-1，x₂=-7 D、x₁=1，x₂=-7

查看试题解析
8. 如图，△ABC是⊙O的内接三角形，∠A=30°，BC=2，则⊙O的直径长为（）

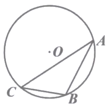A、2 B、 $\sqrt{3}$ C、4 D、8

查看试题解析
9. 一组数1，1，2，3，5，8，13是“斐波那契数列”的一部分，若去掉其中的两个数后，这组数的中位数、众数保持不变，则去掉的两个数可能是（）

A、2，5 B、1，5 C、2，3 D、5，8

查看试题解析
10. 如图，在边长为 $\sqrt{3}$ 的正方形ABCD中，点E是边AD上的一点，连结BE，将△ABE绕着点B顺时针旋转一定的角度，使得点A落在线段BE上，记为点F，此时点E恰好落在边CD上，记为点G，则AE的长为（）

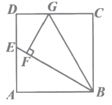A、 $\frac{3 \sqrt{3}}{5}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\sqrt{2}$ D、1

查看试题解析
11. 下列尺规作图中，能确定圆心的是（）
①如图1，在圆上任取三个点A，B，C，分别作弦AB，BC的垂直平分线，交点O即为圆心；②如图2，在圆上任取一点B，以B为圆心，小于直径长为半径画弧交圆于A，C两点，连结AB，BC，作∠ABC的平分线交圆于点D，作弦BD的垂直平分线交BD于点O，点O即为圆心；③如图3，在圆上截取弦AB=CD，连结AB，BC，CD，分别作∠ABC与∠DCB的平分线，交点O即为圆心．

A、①② B、①③ C、②③ D、①②③

查看试题解析
12. 已知点A(t，y₁)，B(t+2，y₂)在抛物线y= $\frac{1}{2} x^{2}$ 的图象上，且-2<t<2，则线段AB长的最大值、最小值分别是（）

A、 $2 \sqrt{5}$ ，2 B、 $2 \sqrt{5}$ ， $2 \sqrt{2}$ C、 $2 \sqrt{10}$ ，2 D、 $2 \sqrt{10}$ ， $2 \sqrt{2}$

查看试题解析

二、填空题(每小题4分，共24分)

13. 因式分解：a²-2a= ．

查看试题解析
14. 一个圆锥的底面半径长为6cm，母线长为10cm，则这个圆锥的侧面积为cm² ．

查看试题解析
15. 等腰直角△ABO在平面直角坐标系中如图所示，点O为坐标原点，直角顶点A的坐标为(2，4)，点B在反比例函数y= $\frac{k}{x}$ (x>0)的图象上，则k的值为．

查看试题解析
16. 如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，DE∥BC，DF∥AC， $\frac{A D}{B D} = \frac{2}{3}$ ，△BDF的面积为9，则四边形DFCE的面积为．

查看试题解析
17. 如图，在4×4的正方形网格图中，以格点为圆心各画四条 $\frac{1}{4}$ 圆弧，则这四条圆弧所围成的阴影部分面积为．

查看试题解析
18. 如图，在菱形ABCD中，AB=5，tanD= $\frac{3}{4}$ ，点E在BC上运动(不与B，C重合)，将四边形AECD沿直线AE翻折后，点C落在C’处，点D落在D’处，C’D’与AB交于点F，当C'D’⊥AB时，CE长为．

查看试题解析

三、解答题(本大题有8小题，共78分)

19. 先化简，再求值：( $\frac{a}{a - 1}$ +1)(a-1)，其中a= $\frac{1}{2}$ ．

查看试题解析
20. “数学来源于生活，又运用于生活”．曹老师为了了解所教班级学生利用数学解决实际问题的能力，编制若干问题对全班学生进行了一次测试，并将测试结果分成四类，A：特别强；B：强；C：一般；D：较弱．以下是由调查测试结果绘制的两幅不完整的统计图，请你根据统计图完成以下解答．

(1)、曹老师的班级共有名学生；

(2)、将下面条形统计图的C类部分补充完整；

(3)、扇形统计图中，D类对应的圆心角为多少度．

查看试题解析
21. 如图，△ABC是正方形网格图中的格点三角形(顶点在格点上)，请分别在图1，图2的正方形网格内按下列要求画一个格点三角形．

(1)、在图1中，以AB为边画直角三角形△ABD(D与C不重合)，使它与△ABC全等：

(2)、在图2中，以AB为边画直角三角形△ABE，使它的一个锐角等于∠B，且与△ABC不全等．

查看试题解析
22. 如图，二次函数图象的顶点为(-1，1)，且与反比例函数的图象交于点A(-3，-3)．

(1)、求二次函数与反比例函数的解析式；

(2)、判断原点(0，0)是否在二次函数的图象上，并说明理由；

(3)、根据图象直接写出二次函数的值小于反比例函数的值时，自变量x的取值范围．

查看试题解析
23. 为了增强体质，小明计划晚间骑自行车训练，他在自行车上安装了夜行灯．如图，夜行灯A射出的光线AB、AC与地面MN的夹角分别为10°和14°，该夜行灯照亮地面的宽度BC长为 $\frac{14}{9}$ 米，求该夜行灯距离地面的高度AN的长．(参考数据：sin10°≈ $\frac{17}{100}$ ，tan10°≈ $\frac{9}{50}$ ，sin14°≈ $\frac{6}{25}$ ，tan14°≈ $\frac{1}{4}$ )．

查看试题解析
24. “2019宁波国际山地马拉松赛”于2019年3月31日在江北区举行．小林参加了环绕荪湖8km的迷你马拉松项目(如图1)，上午8：00起跑，赛道上距离起点5km处会设置饮水补给站．在比赛中，小林匀速前行，他距离终点的路程s(km)与跑步的时间t(h)的函数图象的一部分如图2所示．

(1)、求小林从起点跑向饮水补给站的过程中s与t的函数表达式；

(2)、求小林跑步的速度，以及图2中a的值：

(3)、当跑到饮水补给站时，小林觉得自己跑得太悠闲了，他想挑战自己在上午8：55之前跑到终点，那么接下来一段路程他的速度至少应为多少?

查看试题解析
25. 平行四边形ABCD的对角线相交于点M，△ABM的外接圆交AD于点E，且圆心O恰好落在AD边上，连结ME，若∠BCD=45°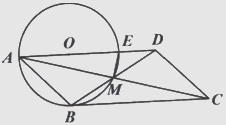

(1)、求证：BC为⊙O切线；

(2)、求∠ADB的度数；

(3)、若朋ME=1，求AC的长．

查看试题解析
26. 等边△ABC与正方形DEFG如图1放置，其中D，E两点分别在AB，BC上，且BD=BE．

(1)、求∠DEB的度数；

(2)、当正方形DEFG沿着射线BC方向以每秒1个单位长度的速度平移时，CF的长度y随着运动时间t变化的函数图象如图2所示，且当t= $\sqrt{3}$ 时，y有最小值1；
①求等边△ABC的边长；

②连结CD，在平移的过程中，求当△CEF与△CDE同时为等腰三角形时t的值；

③从平移运动开始，到GF恰落在AC边上时，请直接写出△CEF外接圆圆心的运动路径的长度．

查看试题解析