浙江省嘉兴市十校联考2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2019-05-23 类型:期中考试
一、选择题(本大题共10题,每小题3分,共30分)
-
1. 在代数式 和 中,x均可以取的值为( )A、9 B、3 C、0 D、-22. 方程3x2=0的根是( )A、x=0 B、x1=x2=0 C、x=3 D、x1= ,x2=-3. 如图,图形中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 = + B、3 - =3 C、 × =7 D、 ÷ =25. 用配方法解一元二次方程x2-8x+2=0,此方程可化为的正确形式是( )A、(x-4)2=14 B、(x-4)2=18 C、(x+4)2=14 D、(x+4)2=186. 对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设( )A、a⊥c B、b⊥c C、a与c相交 D、b与c相交7. 若一组数据x1+1,x2+1,…,xn+1的平均数为17,方差为2,则另一组数据x1+2,x2+2,…,xn+2的平均数和方差分别为( )A、17,2 B、18,2 C、17,3 D、18,38. 新华商场销售某种冰箱,每台进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,设每台冰箱的降价x元,则x满足的关系式为( )A、(x-2500)(8+4× )=5000 B、(2900-x-2500)(8+4× )=5000 C、(x-2500)(8+4× )=5000 D、(2900-x)(8+4× )=50009. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3 .其中正确的结论有( )
4. 下列计算正确的是( )A、 = + B、3 - =3 C、 × =7 D、 ÷ =25. 用配方法解一元二次方程x2-8x+2=0,此方程可化为的正确形式是( )A、(x-4)2=14 B、(x-4)2=18 C、(x+4)2=14 D、(x+4)2=186. 对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设( )A、a⊥c B、b⊥c C、a与c相交 D、b与c相交7. 若一组数据x1+1,x2+1,…,xn+1的平均数为17,方差为2,则另一组数据x1+2,x2+2,…,xn+2的平均数和方差分别为( )A、17,2 B、18,2 C、17,3 D、18,38. 新华商场销售某种冰箱,每台进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,设每台冰箱的降价x元,则x满足的关系式为( )A、(x-2500)(8+4× )=5000 B、(2900-x-2500)(8+4× )=5000 C、(x-2500)(8+4× )=5000 D、(2900-x)(8+4× )=50009. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3 .其中正确的结论有( )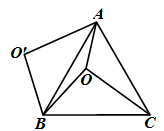 A、1个 B、2个 C、3个 D、4个10. 如图,在△ABC中,BC=a.作BC边的三等分点C1 , 使得CC1∶BC1=1∶2,过点C1作AC的平行线交AB于点A1 , 过点A1作BC的平行线交AC于点D1 , 作BC1边的三等分点C2 , 使得C1C2∶BC2=1∶2,过点C2作AC的平行线交AB于点A2 , 过点A2作BC的平行线交A1C1于点D2;如此进行下去,则线段AnDn的长度为( )
A、1个 B、2个 C、3个 D、4个10. 如图,在△ABC中,BC=a.作BC边的三等分点C1 , 使得CC1∶BC1=1∶2,过点C1作AC的平行线交AB于点A1 , 过点A1作BC的平行线交AC于点D1 , 作BC1边的三等分点C2 , 使得C1C2∶BC2=1∶2,过点C2作AC的平行线交AB于点A2 , 过点A2作BC的平行线交A1C1于点D2;如此进行下去,则线段AnDn的长度为( )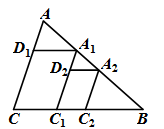 A、 a B、 a C、 a D、 a
A、 a B、 a C、 a D、 a二、填空题(本大题共10题,每小题3分,共30分)
-
11. 一组数据-2,3,2,1,-2的中位数为 .12. 一个多边形的每一个外角都等于36°,这个多边形是 .13. 中国“一带一路”倡议给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年年收入300美元,预计2018年年收入将达到1500美元,设2016年到2018年该地区居民年人均收入平均增长率为x,可列方程为 .14. 四边形ABCD中,∠A+∠B=180°,添加一个条件 , 则使四边形ABCD成为平行四边形.15. 已知关于x的一元二次方程x2+2x+m=0有实数根,则m的取值范围是.
16. 如图,在▱ABCD中,对角线AC,BD交于点O,已知AD=8,BD=14,AC=6,则△OBC的周长为 .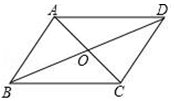 17. 已知3 ,a ,4, b, 5这五个数据,其中a,b是方程x2+2=3x的两个根,那么这五个数据的平均数是 , 方差是 .18. 已知:y为实数,且y<4,则|y-4|- 的化简结果为 .19. 对于实数a,b,定义运算“*”,a*b= 例如4*2.因为4>2,所以4*2=42-4×2=8,若x1、x2是一元二次方程x2-9x+20=0的两个根,则x1*x2= .20. 如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是平行四边形,点A、B、C的坐标分别为A(0,4),B(-2,0),C(8,0),点E是BC的中点,点P为线段AD上的动点,若△BEP是以BE为腰的等腰三角形,则点P的坐标为 .
17. 已知3 ,a ,4, b, 5这五个数据,其中a,b是方程x2+2=3x的两个根,那么这五个数据的平均数是 , 方差是 .18. 已知:y为实数,且y<4,则|y-4|- 的化简结果为 .19. 对于实数a,b,定义运算“*”,a*b= 例如4*2.因为4>2,所以4*2=42-4×2=8,若x1、x2是一元二次方程x2-9x+20=0的两个根,则x1*x2= .20. 如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是平行四边形,点A、B、C的坐标分别为A(0,4),B(-2,0),C(8,0),点E是BC的中点,点P为线段AD上的动点,若△BEP是以BE为腰的等腰三角形,则点P的坐标为 .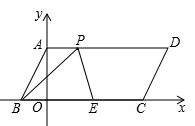
三、解答题(本大题共6个小题,第21~24题每题6分,第25、26题每题8分,共40分)
-
21. 计算: + - .22. 解下列方程(每小题3分,共6分)(1)、(3x+2)2=4;(2)、3x2+1=4x.23. 如图,△ABC中,点D,E分别是边AB,AC的中点,过点C作CF∥AB交DE的延长线于点F,连结BE.
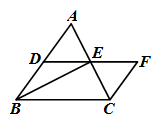 (1)、求证:四边形BCFD是平行四边形.(2)、当AB=BC时,若BD=2,BE=3,求AC的长.24. 某中学九年级组织了一次数学计算比赛(禁用计算器),每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图,请根据提供的信息解答下列问题.
(1)、求证:四边形BCFD是平行四边形.(2)、当AB=BC时,若BD=2,BE=3,求AC的长.24. 某中学九年级组织了一次数学计算比赛(禁用计算器),每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图,请根据提供的信息解答下列问题. (1)、把一班竞赛成绩统计图补充完整.(2)、填表:
(1)、把一班竞赛成绩统计图补充完整.(2)、填表:平均数(分)
中位数(分)
众数(分)
一班
85
二班
84
75
(3)、请从以下给出的两个方面对这次比赛成绩的结果进行分析:①从平均数、众数方面来比较一班和二班的成绩;②从B级以上(包括B级)的人数方面来比较一班和二班的成绩.25. 某市创建“绿色发展模范城市”,针对境内江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内江水水质明显改善.(1)、求n的值;(2)、从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;(3)、该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加一个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年用甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5,求第一年用甲方案治理降低的Q值及a的值.26. 已知在四边形ABCD中,∠A=∠C=90°.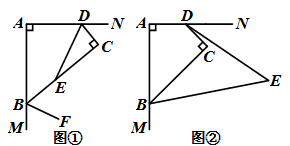 (1)、∠ABC+∠ADC=°;(2)、如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;(3)、如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE= ∠CDN,∠CBE= ∠CBM),试求∠E的度数.
(1)、∠ABC+∠ADC=°;(2)、如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;(3)、如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE= ∠CDN,∠CBE= ∠CBM),试求∠E的度数.