浙江省嘉兴市十校联考2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2019-05-23 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. ∠B的同位角可以是（）．

A、∠1 B、∠2 C、∠3 D、∠4

查看试题解析
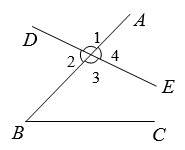
2. 计算 $a^{3} \cdot {(a^{3})}^{2}$ 的结果是（）

A、a⁸ B、a⁹ C、 $a^{11}$ D、 $a^{18}$

查看试题解析
3. 若 ${\begin{cases} x = - 1 \\ y = 2 \end{cases}$ 是关于x ． y的方程 $2 x - y + 2 a = 0$ 的一个解，则常数a为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 如图，AB∥CD，∠C＝70°，BE⊥BC，则∠ABE等于（）

A、20° B、30° C、35° D、60°

查看试题解析
5. 生物学家发现了一种病毒的长度约为0.00000432毫米，数据0.00000432用科学记数法表示为（）

A、4.32×10^-5 B、4.32×10^-6 C、4.32×10⁵ D、4.32×10⁶

查看试题解析
6. 下列运算正确的是（）

A、x²+x³=x⁵ B、 $a^{6} \div a^{3} = a^{2}$ C、 ${(- 2 a^{2})}^{3} = - 8 a^{6}$ D、 $(a + b) (- a - b) = - a^{2} - b^{2}$

查看试题解析
7. 若 $(x + 1) (x^{2} - 5 a x + a)$ 的乘积中不含x²项，则a的值为（）

A、5 B、 $\frac{1}{5}$ C、- $\frac{1}{5}$ D、-5

查看试题解析
8. 如图，已知DC∥FP，∠1＝∠2，∠FED＝32°， ∠AGF＝76°，FH平分∠EFG，则∠PFH的度数是（）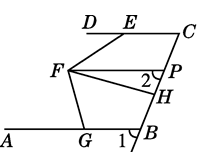

A、54° B、44° C、32° D、22°

查看试题解析
9. 如图，在边长为a的大正方形中剪去一个边长为b的小正方形，再将图中的阴影部分剪拼成一个长方形，若这个拼成的长方形的长为35，宽为15，则图中Ⅱ部分的面积是（）

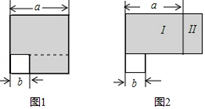A、100 B、125 C、150 D、175

查看试题解析
10. 定义一种对正整数n的“F”运算：①当n是奇数时，F(n)=3n+1；当n为偶数时，F(n)= $\frac{n}{2^{k}}$ （其中k是使 $\frac{n}{2^{k}}$ 为奇数的正整数）……，两种运算交替重复进行. 例如，取n=24，则：

若n=13，则第2018次“F运算”的结果是（）

A、1 B、4 C、2018 D、4²⁰¹⁸

查看试题解析

二、填空题（本大题共10小题，每小题3分，共30分）

11. 计算： $2 x^{2} y^{3} \div (- 3 x y)$ = ．

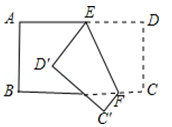
查看试题解析
12. 已知方程2x+y=10 ，用含x的代数式表示y ，则y= ．

查看试题解析
13. 若x²﹣mx+16是一个完全平方式，则m=.

查看试题解析
14. 已知方程组 ${\begin{matrix} a x + b y = 4 \\ b x + a y = 5 \end{matrix}$ 的解是 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ ，则a＋b的值为．

查看试题解析
15. 已知 $2 x + 5 y - 3 = 0$ ，则 $4^{x} • 32^{y} =$ .

查看试题解析
16. 如图，把一个矩形纸片ABCD沿EF折叠后，点D、C分别落在D′、C′的位置．若∠EFB=α，则∠AED′=.

查看试题解析
17. 某年级学生共有246人，男生人数比女生人数的2倍少3人，问男女生各多少人？若设女生人数为x人数，男生人数y人，则可列方程组为.

查看试题解析
18. 计算： $3 (4 + 1) (4^{2} + 1) (4^{4} + 1) (4^{8} + 1) + 1$ ＝.

查看试题解析
19. 已知 $a b = 2019, a - b = 1$ ，那么 $a^{2} + b^{2} =$ .

查看试题解析
20. 已知当x=2时，代数式 $a x^{5} + b x^{3} + c x + 3$ 的值为100，那么当 $x = - 2$ 时，代数式 $a x^{5} + b x^{3} + c x + 3$ =.

查看试题解析

三、解答题（本大题共6小题，共40分）

21.

(1)、计算： $\sqrt{9} - {(π - 3)}^{0} + {(- \frac{1}{3})}^{- 1}$ ；

(2)、化简： $(- 2 x y) • 3 x^{} y^{2} + {(2 x^{2} y)}^{3} \div {(x^{2})}^{2}$ .

查看试题解析
22. 解方程组

(1)、 ${\begin{cases} x = y - 1 \\ 2 y - 3 x = 1 \end{cases}$

(2)、 ${\begin{cases} 2 x + 3 y = 16 \\ 3 x - 2 y = 11 \end{cases}$

查看试题解析
23. 先化简，再求值。
${(3 a + b)}^{2} - (3 a - b) (3 a + b) - 5 b (a - b)$ （其中 $a = 1, b = - 2$ ）

查看试题解析
24. 已知，AC⊥AB，EF⊥BC，AD⊥BC，∠1=∠2，请问AC⊥DG吗？请写出推理过程．

查看试题解析
25. 越来越多的人在用微信支付、转账，把微信账户里的钱转到银行卡叫做提现，自2016年3月1日起，每个微信账户终身享有1000元的免费提现额度，当累计提现金额超过1000元时，累计提现金额超出1000的部分需支付0.1%的手续费，以后每次提现支付的手续费为提现金额的0.1%.

(1)、小明在今天第1次进行了提现，金额为1800元，他需支付手续费元；

(2)、小亮自2016年3月1日至今，用自己的微信账户共提现3次，3次提现金额和手续费分别如下，问：小明3次提现金额共计多少元？

第1次

第2次

第3次

提取金额（元）

a

b

3a+2b

手续费（元）

0

0.4

3.4

查看试题解析
26. 已知直线AB∥CD．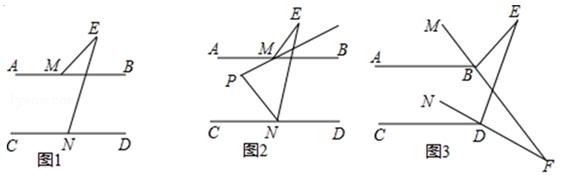

(1)、如图1，直接写出∠BME、∠E、∠END的数量关系为；

(2)、如图2，∠BME与∠CNE的角平分线所在的直线相交于点P，试探究∠P与∠E之间的数量关系，并证明你的结论；

(3)、如图3， $∠ A B M = \frac{1}{n} ∠ M B E ， ∠ C D N = \frac{1}{n} ∠ N D E$ ，直线MB、ND交于点F ，则 $\frac{∠ F}{∠ E}$ =(直接写出结果）

查看试题解析

	第1次	第2次	第3次
提取金额（元）	a	b	3a+2b
手续费（元）	0	0.4	3.4