广西北部湾经济区六市2019年同城学科九年级数学素养测试
试卷更新日期:2019-05-23 类型:中考模拟
一、选择题(共12小题,每小题3分,共36分.)
-
1. -2的绝对值是( )A、-2 B、- C、 D、2
-
2. 如图所示的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
3. 点P(-1,2)所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
4. 下列成语中,表示必然事件的是( )A、旭日东升 B、守株待兔 C、水中捞月 D、刻舟求剑
-
5. 如图,平行线AB,CD被直线AE所截,若∠1=110°,则∠2等于( )
 A、70° B、80° C、90° D、110°
A、70° B、80° C、90° D、110° -
6. 2018年,中国青年科学家李栋首创的新型超分辨成像技术,使显微镜的分辨率达到0.000000097m.其中数据0.000000097用科学记数法表示是( )A、0.97×10-7 B、9.7×10-8 C、0.97×107 D、9.7×108
-
7. 下列运算正确的是( )A、a2 . a4=a8 B、a6÷a3=a2 C、(ab)2=a2b2 D、(a4)2=a6
-
8. 某校对学生“一周课外阅读时间”的情况进行随机抽样调查,调查结果如统计图所示.若该校有2000名学生,则根据调查结果可估算该校学生一周阅读时间不足3小时的人数是第( )
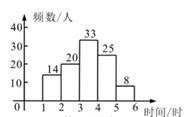 A、280人 B、400人 C、660人 D、680人
A、280人 B、400人 C、660人 D、680人 -
9. 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=4,观察图中尺规作图的痕迹,则AD的长是( )
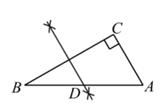 A、4 B、4 C、2 D、2
A、4 B、4 C、2 D、2 -
10. 将一块长方形桌布铺在长为3m,宽为2m的长方形桌面上,各边下垂的长度相同,且桌布的面积是桌面面积的2倍,求桌布下垂的长度.设桌布下垂的长度为xm,则所列的方程是( )A、(2x+3)(2x+2)=2×3×2 B、2(x+3)(x+2)=3×2 C、(x+3)(x+2)=2×3×2 D、2(2x+3)(2x+2)=3×2 21/4x
-
11. 二次函数y=ax2+bx+c的图象如图所示,下列结论:
①a<0;②ax2+bx+c=0的两个根是x1=-2,x2=4;
③9a+c>0;④b:c=1:4,其中正确的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
12. 如图,△ABC是⊙O的内接三角形,把 沿BC折叠后,与弦AB交于点P,恰好OP⊥AB.若OP=1,AB=4,则BC:AC等于( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题(本大题共6小题,每小题3分,共18分.)
-
13. 比较大小:-30.(填“>”“<”或“=”)
-
14. 若分式 有意义,则x的取值范围是。
-
15. 如图,用一张半径为10cm的扇形纸板做一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的高为8cm,那么这张扇形纸板的弧长是 cm.

-
16. 在一个不透明袋子中装有除颜色外无其他差别的红球2个,绿球3个,从中随机摸出一个球,放回并摇匀,再随机摸出一个球,则两次摸出的球中“有一个红球,一个绿球”的概率是 .
-
17. 如图,在矩形OABC中,OA=2,OC=4,F是BC边的一个动点(F不与B,C重合).过点F的反比例函数y= (k>0)的图象与AB边交于点E,使△EFC的面积最大的k的值是 .

-
18. 如图,把Rt△OAB置于平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(3,0),点P是Rt△OAB内切圆的圆心.将Rt△OAB沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后圆心为P1 , 第二次滚动后圆心为P2 , …,依此规律,第2019次滚动后,Rt△OAB内切圆的圆心P2019的坐标是 .

三、解答题(本大题共8小题,共66分.解答应写出文字说明,证明过程或演算步骤。)
-
19. 计算:(-5)×2-(-3)+(-2)2÷4.
-
20. 先化简,再求值: ,其中x= -2.
-
21. 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,1),B(-4,1),C(-2,3)
①画出△ABC关于点O成中心对称的△A1B1C1;
②以点A为位似中心,将△ABC放大为原来的2倍,得到△AB2C2 , 请在第二象限内画出△AB2C2;
③直接写出以点A1 , B1 , C1为顶点,以A1B1为一边的平行四边形的第四个顶点D的坐标.
-
22. 某校为了对甲,乙两名同学进行学生会主席的竞选考核,召开了一次竞选答辩及民主测评会.由A,B,C,D,E五位教师评委对竞选答辩进行评分,并选出20名学生代表参加民主投票.竞选答辩的结果如下表所示:
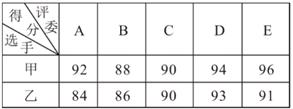

民主投票的结果为:甲8票,乙12票。
根据以上信息解答下列问题:
(1)、甲,乙两人的竞选答辩得分分别是多少?(2)、如果综合得分=竞选答辩得分+民主投票得分,那么,甲,乙两人谁当选学生会主席?(3)、如果综合得分=竞选答辩得分xa+民主投票得分×(1-a),那么,当a=0.6时,甲,乙两人谁当选学生会主席? -
23. 清泉阁是南宁园博园中的最高建筑.某数学兴趣小组利用周末到清泉阁进行室外测量实践活动.如图,在清泉阁最大的观景台上,选取测量点D,测得点D到清泉阁最高点A的仰角∠ADE=58°,点D到目标点C的俯角∠FDC=32°,DE=20m.已知清泉阁的高AB=75m,请计算测量点D到目标点C的距离(结果取整数).(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
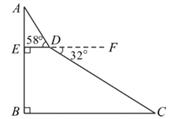
-
24. 广西“稻鱼综合养殖”符合生态养殖,绿色发展.某稻鱼综合养殖户计划购买甲,乙两种禾花鱼鱼苗,经调查,得到以下信息:
购买重量小于40kg
购买重量不小于40kg
甲鱼苗
原价销售
打七折销售
乙鱼苗
原价销售
打八折销售
如果购买10kg的甲鱼苗和5kg的乙鱼苗需用700元,如果购买20kg的甲鱼苗和15kg的乙鱼苗需用1600元。
(1)、甲鱼苗和乙鱼苗的单价各是多少元?(2)、现决定购买甲,乙两种鱼苗共90kg,其中,乙鱼苗的重量不大于甲鱼苗重量的2倍,设购买甲鱼苗akg(a≤50),求该养殖户购买这批鱼苗的总费用W与a之间的函数解析式;(3)、在(2)的条件下,请设计一种购买方案,使所需总费用最低,并求出最低总费用. -
25. 在菱形ABCD中,∠MDN的两边分别与AB,BC交于点E,F,与对
角线AC交于点G,H,已知∠MDN=∠BAD=60°,AC=6.
(1)、如图1,当DE⊥AB,DF⊥BC时,①求证:△ADE≌△CDF;
②求线段GH的长;
(2)、如图2,当∠MDN绕点D旋转时,线段AG,GH,HC的长度都在变化.设线段AG=m,GH=p,HC=n,试探究p与mn的等量关系,并说明理由.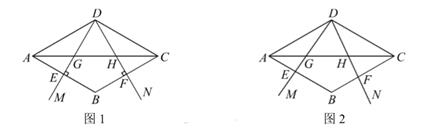
-
26. 如图,在平面直角坐标系中,抛物线y=a(x+5)(x-3)与x轴交于A,B两点(点A在点B的左侧),且过点(-2,4).

(1)、直接写出a的值和点B的坐标;(2)、将抛物线向右平移2个单位长度,所得的新抛物线与x轴交于M,N两点,两抛物线交于点P,求点M到直线PB的距离;
(3)、在(2)的条件下,若点D为直线BP上的一个动点,是否存在点D,使得∠DAB= ∠PBA?若存在,请求出点D的坐标;若不存在,请说明理由.
