江苏省张家港市2019年中考网上阅卷适应性考试数学试卷
试卷更新日期:2019-05-23 类型:中考模拟
一、选择题:(本大题共10小题,每小题3分,共30分)
-
1. 下列四个数中,是正整数的是( )A、-2 B、 C、 D、102. 下列计算正确的是( )A、 B、 C、 D、3. 已知某新型感冒病毒的直轻约为0.000000823米,将0.000000823用科学记数法表示( )A、 B、 C、 D、4. 如图,AB是⊙0的直径,PA切⊙O于点A,线段P0交⊙0于点C,连结BC.若∠P=40°,则∠B等于( )
 A、15° B、20° C、25° D、30°5. 某体育用品商店一天中卖出某种品牌的运动鞋15双,其中各种尺码的鞋的销售量如下表所示:( )
A、15° B、20° C、25° D、30°5. 某体育用品商店一天中卖出某种品牌的运动鞋15双,其中各种尺码的鞋的销售量如下表所示:( )鞋的尺码/cm
23
23.5
24
24.5
25
销售量/双
1
3
3
6
2
则这15双鞋的尺码组成的一组数据中,众数和中位数分別为
A、24.5,24.5 B、24.5,24 C、24,24 D、23.5,246. 化简 的结果是( )A、-x2 B、x2 C、-1 D、17. 如图,在Rt△ABC中,CD是斜边AB上的中线.已知AC=3,CD=2,则tanA的值为( ) A、 B、 C、 D、8. 一元二次方程 根的情况是( )
A、 B、 C、 D、8. 一元二次方程 根的情况是( )
A、无实数根 B、有一个正根,一个负根 C、有两个正根,且都小于3 D、有两个正根,且有一根大于39. 如图,平行四边形ABCD绕点D逆时针旋转40°,得到平行四边形A'B'C'D(点A'是A点的对应点,点B’是B点的对应点,点C'是C点的对应点),并且A'点恰好落在AB边上,则∠B的度数为( ) A、100° B、105° C、110° D、115°10. 如图,Rt△ABC中.∠BAC=90°,AB=1,AC= .点D,E分别是边BC.AC上的动点,则DA+DE的最小值为( )
A、100° B、105° C、110° D、115°10. 如图,Rt△ABC中.∠BAC=90°,AB=1,AC= .点D,E分别是边BC.AC上的动点,则DA+DE的最小值为( )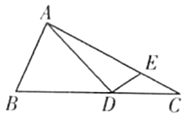 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:(本大题共8小题,毎小题3分,共24分)
-
11. 计算:12. 分式方程 的解为13. 若 ,则14. 已知直线 //b,将一块含45°角的直角三角板(∠C=90°),按如图所示的位置摆放,若∠1=55°,则∠2的度数为
 15. 如图,正六边形内接于⊙O,小明向圆内投掷飞镖一次,则飞镖落在阴影部分的概率是 .
15. 如图,正六边形内接于⊙O,小明向圆内投掷飞镖一次,则飞镖落在阴影部分的概率是 . 16. 如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏东60°方向行驶12千米至B地,再沿北偏西45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,则B,C两地的距离为千米。(结果保留根号)
16. 如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏东60°方向行驶12千米至B地,再沿北偏西45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,则B,C两地的距离为千米。(结果保留根号) 17. 如图,正方形ABCD中,AB=6,E是CD的中点,将△ADE沿AE翻折至△AFE,连接CF,则CF的长度是
17. 如图,正方形ABCD中,AB=6,E是CD的中点,将△ADE沿AE翻折至△AFE,连接CF,则CF的长度是 18. 甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示。给出下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7 ,80) ;④n=7.5.其中说法正确的有. (把你认为正确结论的序号都填上)
18. 甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示。给出下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7 ,80) ;④n=7.5.其中说法正确的有. (把你认为正确结论的序号都填上)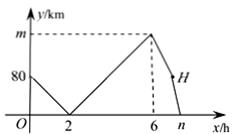
三、解答题:(本大题共10小题,共76分)
-
19. 计算:20. 解不等式组:
21. 一只不透明的口袋里装有1个红球、1个黄球和若干个白球,这些球除颜色外其余都相同,搅匀后从中任意摸出一个是白球的概率为(1)、试求袋中白球的个数(2)、搅匀后从中任意摸出1个球(不放回),再从余下的球中任意摸出1个球,试用画树状图或列表格的方法,求两次摸出的2个球恰好是1个白球、1个红球的概率,22. 在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F. (1)、证明: ;(2)、若∠CDF=30°,且AB=3,求AE的长。23. 为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表。
(1)、证明: ;(2)、若∠CDF=30°,且AB=3,求AE的长。23. 为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表。
请根据以上图表,解答下列问题:
(1)、填空:这次被调查的同学共有人,a+b=. m=;(2)、求扇形统计图中扇形C的圆心角度数:(3)、该校共有1000人,请估计每月零花钱的数额 在60≤ <120范围的人数。24. 某学校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元(1)、求每个篮球和每个足球的售价:(2)、如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?25. 如图,反比例函数 的图像经过A(1,3),B(m,n),其中m>1.过点B作y轴的垂线,垂足为C.连接AB,AC,△ABC的面积为 (1)、求k的值和直线AB的函数表达式:(2)、过线段AB上的一点P作PD⊥ 轴于点D,与反比例函数 的图像交于点E,连接OP,OE,若△POE的面积为1,求点P的坐标.26. 如图,以△ABC的BC边上一点O为圆心的圆,经过A、C两点,与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F.AB=BF,CF=4,DF= .
(1)、求k的值和直线AB的函数表达式:(2)、过线段AB上的一点P作PD⊥ 轴于点D,与反比例函数 的图像交于点E,连接OP,OE,若△POE的面积为1,求点P的坐标.26. 如图,以△ABC的BC边上一点O为圆心的圆,经过A、C两点,与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F.AB=BF,CF=4,DF= . (1)、求证:AB是⊙O的切线;(2)、求⊙O的半径r.(3)、设点P是BA延长线上的一个动点,连接DP交CF于点M,交弧AC于点N(N与A、C不重合).试问 是否为定值?如果是,求出该定值:如果不是.请说明理由。27. 如图,在四边形ABCD中,AB// DC,CB⊥AB.AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s。点P和点Q同时出发,设运动的时间为t(s),0<t<5.
(1)、求证:AB是⊙O的切线;(2)、求⊙O的半径r.(3)、设点P是BA延长线上的一个动点,连接DP交CF于点M,交弧AC于点N(N与A、C不重合).试问 是否为定值?如果是,求出该定值:如果不是.请说明理由。27. 如图,在四边形ABCD中,AB// DC,CB⊥AB.AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s。点P和点Q同时出发,设运动的时间为t(s),0<t<5. (1)、用含t的代数式表示AP;(2)、当以点A.P,Q为顶点的三角形与△ABD相似时,求t的值;(3)、当QP⊥BD时,求t的值28. 如图1,抛物线 与 相交于点O、C, 与 分别交x轴于点B、A,且B为线段AO的中点.
(1)、用含t的代数式表示AP;(2)、当以点A.P,Q为顶点的三角形与△ABD相似时,求t的值;(3)、当QP⊥BD时,求t的值28. 如图1,抛物线 与 相交于点O、C, 与 分别交x轴于点B、A,且B为线段AO的中点. (1)、点A的坐标为( , ),点B的坐标为( , ), 的值为;(2)、若OC⊥AC,求△OAC的面积;(3)、在(2)的条件下,设抛物线 的对称轴为 ,顶点为M(如图2),点E在抛物线 上点O与点M之间运动,四边形OBCE的面积是否存在最大值?若存在,求出面积的最大值和点E的坐标;若不存在,请说明理由.
(1)、点A的坐标为( , ),点B的坐标为( , ), 的值为;(2)、若OC⊥AC,求△OAC的面积;(3)、在(2)的条件下,设抛物线 的对称轴为 ,顶点为M(如图2),点E在抛物线 上点O与点M之间运动,四边形OBCE的面积是否存在最大值?若存在,求出面积的最大值和点E的坐标;若不存在,请说明理由.