江苏省常熟市2019学年九年级数学适应性质量监测
试卷更新日期:2019-05-23 类型:中考模拟
一、选择题,本大题共10小题,每小题3分,共30分。
-
1. 下列四个实数中,最大的实数是( )A、 B、 C、0 D、2. 下列四个图案中,不是中心对称图案的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 关于 的一元二次方程 根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定5. 在一个不透明的袋子中放有 个球,其中有6个白球,这些球除颜色外完全相同,若每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0. 25左右,则 的值约为( )A、10 B、15 C、20 D、246. 如图, 是一块直角三角板, , ,现将三角板叠放在一把直尺上, 与直尺的两边分别交于点D,E,AB与直尺的两边分别交于点F,G,若∠1=40°,则∠2的度数为( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 关于 的一元二次方程 根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定5. 在一个不透明的袋子中放有 个球,其中有6个白球,这些球除颜色外完全相同,若每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0. 25左右,则 的值约为( )A、10 B、15 C、20 D、246. 如图, 是一块直角三角板, , ,现将三角板叠放在一把直尺上, 与直尺的两边分别交于点D,E,AB与直尺的两边分别交于点F,G,若∠1=40°,则∠2的度数为( )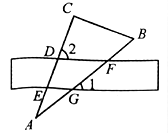 A、40º B、50º C、60º D、70º7. 若 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、 且8. 如图,四边形 内接于⊙ ,连接 , .若 , .则∠ABC的度数为( )
A、40º B、50º C、60º D、70º7. 若 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、 且8. 如图,四边形 内接于⊙ ,连接 , .若 , .则∠ABC的度数为( )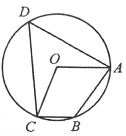 A、110° B、120° C、125° D、135°9. 如图,一艘轮船在 处测得灯塔 在北偏西15º的方向上,该轮船又从 处向正东方向行驶40海里到达 处,测得灯塔 在北偏西60º的方向上,则轮船在 处时与灯塔 之间的距离(即 的长)为( )
A、110° B、120° C、125° D、135°9. 如图,一艘轮船在 处测得灯塔 在北偏西15º的方向上,该轮船又从 处向正东方向行驶40海里到达 处,测得灯塔 在北偏西60º的方向上,则轮船在 处时与灯塔 之间的距离(即 的长)为( )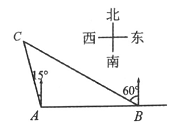 A、 海里 B、 海里 C、80海里 D、 海里10. 小明骑自行车去上学途中,经过先上坡后下坡的一段路,在这段路上所骑行的路程 (米)与时间 (分钟)之间的函数关系如图所示.下列结论:①小明上学途中下坡路的长为1800米;②小明上学途中上坡速度为150米/分,下坡速度为200米/分;③如果小明放学后按原路返回,且往返过程中,上、下坡的速度都相同,则小明返回时经过这段路比上学时多用1分钟;④如果小明放学后按原路返回,返回所用时间与上学所用时间相等,且返回时下坡速度是上坡速度的1.5倍,则返回时上坡速度是160米/分其中正确的有( )
A、 海里 B、 海里 C、80海里 D、 海里10. 小明骑自行车去上学途中,经过先上坡后下坡的一段路,在这段路上所骑行的路程 (米)与时间 (分钟)之间的函数关系如图所示.下列结论:①小明上学途中下坡路的长为1800米;②小明上学途中上坡速度为150米/分,下坡速度为200米/分;③如果小明放学后按原路返回,且往返过程中,上、下坡的速度都相同,则小明返回时经过这段路比上学时多用1分钟;④如果小明放学后按原路返回,返回所用时间与上学所用时间相等,且返回时下坡速度是上坡速度的1.5倍,则返回时上坡速度是160米/分其中正确的有( ) A、①④ B、②③ C、②③④ D、②④
A、①④ B、②③ C、②③④ D、②④二、填空题,本大题共8小题,每小题3分,共24分.
-
11. 的倒数是.12. DNA分子的直径只有0. 000 000 2 cm,将0. 000 000 2用科学记数法可表示为.13. 已知一组数据:5, ,3,6,4的众数是4,则该组数据的中位数是.14. 因式分解: .15. 已知点 是一次函数 的图像与反比例函数 的图像的一个交点,则 的值为.16. 若圆锥的侧面积是其底面积的3倍,则圆锥侧面展开图的圆心角的度数是.17. 如图,在 中, , ,点 是边 上一点(点 不与点 , 重合),将 沿 翻折,点 的对应点是 , 交 于点 ,若 ,则 的长为.
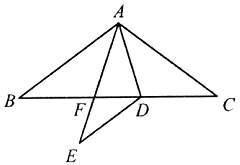 18. 如图,四边形 中, , , , 是对角线,以 为边向四边形内部作正方形 ,连接 ,则 的长为 。
18. 如图,四边形 中, , , , 是对角线,以 为边向四边形内部作正方形 ,连接 ,则 的长为 。
三、解答题,本大题共10小题,共76分.
-
19. 计算: .20. 解不等式组: ,并把它的解集在数轴上表示出来.
 21. 先化简,再求值: ,其中 .22. 如图,平行四边形 中, 是对角线 的中点,过点 的直线 分别交 , 的延长线于 , .
21. 先化简,再求值: ,其中 .22. 如图,平行四边形 中, 是对角线 的中点,过点 的直线 分别交 , 的延长线于 , .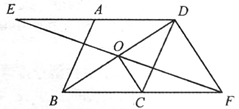 (1)、求证: ;(2)、若 ,试探究线段 与线段 之间的关系,并说明理由.23. 今年4月22 日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
(1)、求证: ;(2)、若 ,试探究线段 与线段 之间的关系,并说明理由.23. 今年4月22 日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题: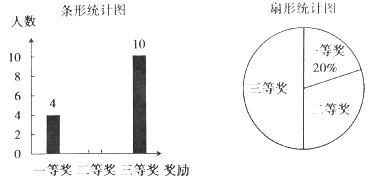 (1)、求本次竞赛获奖的总人数,并补全条形统计图;(2)、求扇形统计图中“二等奖”所对应扇形的圆心角度数;(3)、已知甲、乙、丙、丁4位同学获得一等奖,学校将采取随机抽签的方式在4人中选派2人参加上级团委组织的“爱护环境、保护地球”知识竞赛,请求出抽到的2人恰好是甲和乙的概率(用画树状图或列表等方法求解).24. 为了丰富校园文化生活,促进学生积极参加体育运动,某校准备成立校排球队,现计划购进一批甲、乙两种型号的排球,已知一个甲种型号排球的价格与一个乙种型号排球的价格之和为140元;如果购买6个甲种型号排球和5个乙种型号排球,一共需花费780元.(1)、求每个甲种型号排球和每个乙种型号排球的价格分别是多少元?(2)、学校计划购买甲、乙两种型号的排球共26个,其中甲种型号排球的个数多于乙种型号排球,并且学校购买甲、乙两种型号排球的预算资金不超过1900元,求该学校共有几种购买方案?25. 如图,在平面直角坐标系中,矩形 的顶点 在 轴的正半轴上, . 对角线 相交于点 ,反比例函数 ( )的图像经过点 ,分别与 交于点 .
(1)、求本次竞赛获奖的总人数,并补全条形统计图;(2)、求扇形统计图中“二等奖”所对应扇形的圆心角度数;(3)、已知甲、乙、丙、丁4位同学获得一等奖,学校将采取随机抽签的方式在4人中选派2人参加上级团委组织的“爱护环境、保护地球”知识竞赛,请求出抽到的2人恰好是甲和乙的概率(用画树状图或列表等方法求解).24. 为了丰富校园文化生活,促进学生积极参加体育运动,某校准备成立校排球队,现计划购进一批甲、乙两种型号的排球,已知一个甲种型号排球的价格与一个乙种型号排球的价格之和为140元;如果购买6个甲种型号排球和5个乙种型号排球,一共需花费780元.(1)、求每个甲种型号排球和每个乙种型号排球的价格分别是多少元?(2)、学校计划购买甲、乙两种型号的排球共26个,其中甲种型号排球的个数多于乙种型号排球,并且学校购买甲、乙两种型号排球的预算资金不超过1900元,求该学校共有几种购买方案?25. 如图,在平面直角坐标系中,矩形 的顶点 在 轴的正半轴上, . 对角线 相交于点 ,反比例函数 ( )的图像经过点 ,分别与 交于点 .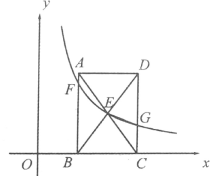 (1)、若 ,求 的值;(2)、连接 ,若 ,求 的面积.26. 如图,在 中, ,以 为直径的⊙ 分别交 于点 ,交 的延长线于点 ,过点 作 ,垂足为点 ,连接 ,交 于点 .
(1)、若 ,求 的值;(2)、连接 ,若 ,求 的面积.26. 如图,在 中, ,以 为直径的⊙ 分别交 于点 ,交 的延长线于点 ,过点 作 ,垂足为点 ,连接 ,交 于点 .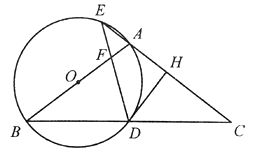 (1)、求证: 是⊙ 的切线;(2)、若⊙ 的半径为4,
(1)、求证: 是⊙ 的切线;(2)、若⊙ 的半径为4,①当 时,求 的长(结果保留π);
②当 时,求线段 的长.
27. 如图①,四边形 是知形, ,点 是线段 上一动点(不与 重合),点 是线段 延长线上一动点,连接 交 于点 .设 ,已知 与 之间的函数关系如图②所示.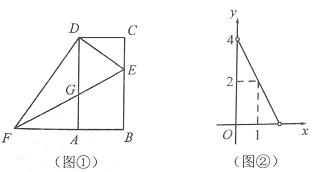 (1)、求图②中 与 的函数表达式;(2)、求证: ;(3)、是否存在 的值,使得 是等腰三角形?如果存在,求出 的值;如果不存在,说明理由28. 如图1,二次函数 的图像与 轴交于 两点(点 在点 的左侧),与 轴交于点 .
(1)、求图②中 与 的函数表达式;(2)、求证: ;(3)、是否存在 的值,使得 是等腰三角形?如果存在,求出 的值;如果不存在,说明理由28. 如图1,二次函数 的图像与 轴交于 两点(点 在点 的左侧),与 轴交于点 .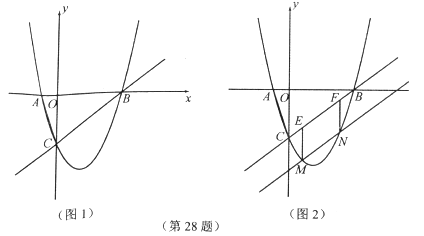 (1)、求二次函数的表达式及点 、点 的坐标;(2)、若点 在二次函数图象上,且 ,求点 的横坐标;(3)、将直线 向下平移,与二次函数图象交于 两点( 在 左侧),如图2,过 作 轴,与直线 交于点 ,过 作 轴,与直线 交于点 ,当 的值最大时,求点 的坐标.
(1)、求二次函数的表达式及点 、点 的坐标;(2)、若点 在二次函数图象上,且 ,求点 的横坐标;(3)、将直线 向下平移,与二次函数图象交于 两点( 在 左侧),如图2,过 作 轴,与直线 交于点 ,过 作 轴,与直线 交于点 ,当 的值最大时,求点 的坐标.