江苏省泰兴市2018-2019年七年级下学期数学期中考试试卷

试卷更新日期：2019-05-23 类型：期中考试

进入出卷网下载

一、选择题（本大题共6小题，每小题2分，共12分）

1. 下列车标，可看作图案的某一部分经过平移所形成的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式从左到右的变形，是因式分解的是（）

A、 $x^{2} - 4 + 4 x = (x + 2) (x - 2) + 4 x$ B、 $(x + 3) (x - 2) = x^{2} + x - 6$ C、 $x^{2} + 6 x + 9 = {(x + 3)}^{2}$ D、 $x^{2} + x + 1 = (x + 1 + \frac{1}{x})$

查看试题解析
3. 下列命题中，是假命题的是（）

A、两直线平行，则同位角相等 B、同旁内角互补，则两直线平行 C、三角形内角和为180° D、三角形一个外角大于任何一个内角

查看试题解析
4. 若 $a + b = 3$ ， $a^{2} - b^{2} = 15$ ，则 $a - b$ 的值为（）

A、12 B、8 C、5 D、3

查看试题解析
5. 若 $(x^{2} + p x + 2) (x - 3)$ 的乘积中不含 $x^{2}$ 项，则p的值为（）

A、3 B、-3 C、 $\pm$ 3 D、无法确定

查看试题解析
6. 已知关于 $x 、 y$ 方程组 ${\begin{matrix} 2 x + 3 y = m \\ 3 x + 2 y = m + 1 \end{matrix}$ 的解满足 $x + y = 3$ ，则m的值为（）

A、10 B、8 C、7 D、6

查看试题解析

二、填空题（本大题共10小题，每小题2分，共20分）

7. 计算 $6 x^{3} \cdot (- 2 x^{2} y)$ ．

查看试题解析
8. 八边形的外角和为．

查看试题解析
9. 写出一个解为 ${\begin{matrix} x = 2 \\ y = - 3 \end{matrix}$ 的二元一次方程组：．

查看试题解析
10. 命题“对顶角相等”的逆命题是

查看试题解析
11. 已知三角形的三边长均为偶数，其中两边长分别为2和8，则第三边长为．

查看试题解析
12. 关于x、y的方程 $(a - 1) x^{| a |} + y = 3$ 是二元一次方程，则a＝．

查看试题解析
13. 如图，CE⊥AF，垂足为E，CE与BF相交于点D，∠F＝45°，∠DBC＝105°，则∠C= ．

查看试题解析
14. 若 $x^{2} + m x + 4 = {(x + n)}^{2}$ （其中m、n为常数），则m的值是．

查看试题解析
15. 如图，△ABC的中线BD、CE相交于点O，OF⊥BC，且AB＝5cm，BC＝4cm，AC＝ $\frac{5}{2}$ cm，OF＝2cm，则四边形ADOE的面积是．

查看试题解析
16. 如图△ABC中，将边BC沿虚线翻折，若∠1+∠2=102°，则∠A的度数是．

查看试题解析

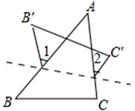
三、解答题（本大题共10小题，共68分）

17. 计算：

(1)、 $3 x (x + 3) - (x + 2) (x - 1)$

(2)、 $(2 x - 1) (2 x + 1) (4 x^{2} - 1)$

(3)、 $100^{2} - 98 \times 102$ (用简便方法)

查看试题解析
18. 把下列各式因式分解:

(1)、 $m^{3} - 16 m$

(2)、 ${(x^{2} + y^{2})}^{2} - 4^{x^{2}} y^{2}$

查看试题解析
19. 解方程组：

(1)、 ${\begin{matrix} x - 2 y = 1 \\ 2 x + 3 y = 9 \end{matrix}$

(2)、 ${\begin{matrix} \frac{x}{2} + \frac{y}{2} = - 2 \\ x - 4 y = 3 \end{matrix}$

查看试题解析
20. 已知 $A = {(2 x - y)}^{2}$ ， $B = 4 x (x - y)$

(1)、求2A-B的值，其中 $x = - 1$ ， $y = 1$ ；

(2)、试比较代数式A、B的大小．

查看试题解析
21. 如图，△ABC的顶点都在方格纸的格点上，将△ABC先向下平移3格，再向右平移2格，得到△A′B′C′；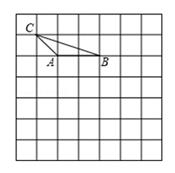

(1)、①请在图中画出平移后的△A′B′C′；
② 在图中画出△ABC的高BD，并标出垂足D；

(2)、若连接AA′，BB′，则这两条线段之间的关系是．

查看试题解析
22. 解方程组 ${\begin{matrix} a x + b y = 2 \\ c x + 5 y = 8 \end{matrix}$ 时，一马虎的学生把写错而得 ${\begin{matrix} x = - 3 \\ y = 1 \end{matrix}$ ，而正确的解是 ${\begin{matrix} x = 3 \\ y = - 2 \end{matrix}$ ，求 $a + b - c$ 的值．

查看试题解析
23. 如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠1＝63°，∠2＝63°，且∠C＝∠D．求证：∠A=∠F．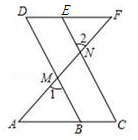

查看试题解析
24. 观察下列各式：
$2 \times 6 + 4 = 4^{2}$ …………①

$4 \times 8 + 4 = 6^{2}$ …………②

$6 \times 10 + 4 = 8^{2}$ …………③

……

探索以上式子的规律：

(1)、试写出第5个等式；

(2)、试写出第n个等式（用含n的式子表示），并用你所学的知识说明第n个等式成立．

查看试题解析
25. 某校准备组织七年级400名学生参加夏令营，已知用3辆小客车和1辆大客车每次可运送学生105人；用1辆小客车和2辆大客车每次可运送学生110人

(1)、每辆小客车和每辆大客车各能坐多少名学生？

(2)、若学校计划租用小客车a辆，大客车b辆，一次送完，且恰好每辆车都坐满
①请写出a、b满足的关系式．
②若小客车每辆租金2000元，大客车每辆租金3800元，请你设计出最省钱的租车方案．

查看试题解析
26.
$△ A B C$ 中，三个内角的平分线交于点O，过点O作 $O D ⊥ O B$ ，交边A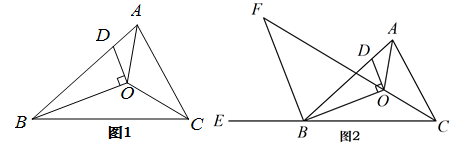B于点D．

(1)、如图1，
①若∠ABC=40°，则∠AOC= ， ∠ADO=；
②猜想∠AOC与∠ADO的关系，并说明你的理由。

(2)、如图2，作∠ABC外角∠ABE的平分线交CO的延长线于点F ．若∠AOC=105°，∠F=32°，则∠AOD=°.

查看试题解析