江苏省泰兴市2018-2019年八年级下学期数学期中考试试卷

试卷更新日期：2019-05-23 类型：期中考试

进入出卷网下载

一、选择题（每题2分，共12分）

1. 下列图形中，是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列分式中，最简分式是（）

A、 $\frac{x^{2} + y^{2}}{x + y}$ B、 $\frac{6 b}{4 a}$ C、 $\frac{x^{2} - 4}{x - 2}$ D、 $\frac{a^{2} + 4 a}{a}$

查看试题解析
3. 下列事件中是必然事件的是（）

A、投掷一枚质地均匀的硬币100次，正面朝上的次数为50次 B、任意一个六边形的外角和等于720° C、如果a²＝b² ，那么a＝b D、13个同学参加一个聚会，他们中至少有两个同学的生日在同一个月

查看试题解析
4. 下列代数式变形正确的是（）

A、 $\frac{x - y}{x^{2} - y^{2}} = \frac{1}{x - y}$ B、 $\frac{- x + y}{2} = - \frac{x + y}{2}$ C、 $\frac{1}{x y} \div (\frac{1}{x} + \frac{1}{y}) = \frac{1}{y} + \frac{1}{x}$ D、 $\frac{x - y}{x + y} = \frac{x^{2} - y^{2}}{{(x + y)}^{2}}$

查看试题解析
5. 如图，△ABC中，∠A＝75°，∠B＝50°，将△ABC绕点C按逆时针方向旋转，得到△A’B’ C，点A的对应点A'落在AB边上，则∠BCA'的度数为（）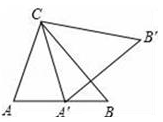

A、20° B、25° C、30° D、35°

查看试题解析
6. 如图，在△ABC中，点D，E，F分别是AB，BC，AC的中点，则下列四个判断中不一定正确的是（）

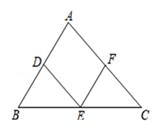A、四边形ADEF一定是平行四边形 B、若∠B+∠C＝90°，则四边形ADEF是矩形 C、若四边形ADEF是菱形，则△ABC是等边三角形 D、若四边形ADEF是正方形，则△ABC是等腰直角三角形

查看试题解析

二、填空题（每题2分，共20分）

7. 分式 $\frac{x}{x - 1}$ 有意义的条件是．

查看试题解析
8. 六张完全相同的卡片上，分别画有等边三角形、正方形、矩形、平行四边形、圆、菱形，现从中随机抽取一张，卡片上画的恰好既是轴对称图形又是中心对称图形的概率为．

查看试题解析
9. 当x＝时，分式 $\frac{x^{2} - 1}{1 - x}$ 的值等于0．

查看试题解析
10. 为了了解我市2018年中考数学学科各分数段成绩分布情况，从中抽取180名考生的中考数学成绩进行统计分析，在这个问题中，样本是指．

查看试题解析
11. 菱形ABCD的周长为52cm，一条对角线的长为24cm，则该菱形的面积为cm² ．

查看试题解析
12. 一只不透明的袋子中装有红球和白球共30个，这些球除了颜色外都相同，校课外学习小组做摸球实验，将球搅匀后任意摸出一个球，记下颜色后放回，搅匀，通过多次重复试验，算得摸到红球的频率是0.2，则袋中有个红球．

查看试题解析
13. 若分式方程 $\frac{m}{x - 3} = \frac{2}{x - 3} + 1$ 有增根，则m= ．

查看试题解析
14. 如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE＝度．

查看试题解析
15. 若分式 $\frac{6}{m - 2}$ 的值是正整数，则m可取的整数有．

查看试题解析
16. Rt△ABC中，∠C＝90°，BC＝4，D为AB中点，点E在AC上，ED平分△ABC的周长，则ED＝．

查看试题解析

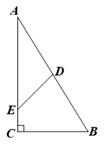
三、解答题

17. 计算：

(1)、 $\frac{3 a}{b} \cdot \frac{a b^{2}}{a^{3} b^{2}} \div \frac{6 b}{a^{2}}$

(2)、 $\frac{1}{2 - x} + \frac{2}{x^{2} - 4} + \frac{1}{2 + x}$

查看试题解析
18. 解方程：

(1)、 $\frac{x}{2 x - 1} = 2 - \frac{3}{1 - 2 x}$

(2)、 $\frac{x + 1}{x - 1} - \frac{4}{x^{2} - 1} = 1$

查看试题解析
19. 先化简，再求值： $(x + 2 - \frac{5}{x - 2}) \div \frac{x - 3}{3 x^{2} - 6 x}$ ，其中 $x$ 满足 $x^{2} + 3 x - 1 = 0$ .

查看试题解析
20. 已知 $\frac{3 x - 2}{(x + 1) (x - 1)} = \frac{A}{x - 1} + \frac{B}{x + 1}$ ，求A、B的值.

查看试题解析
21. 已知△ABC的三个顶点的坐标分别为A（﹣5，0）、B（﹣2，3）、C（﹣1，0）.

(1)、①画出△ABC关于坐标原点O成中心对称的△A₁B₁C₁；
②将△ABC绕坐标原点O顺时针旋转90°，画出对应的△A′B′C′；

(2)、若以A′、B′、C′、D′为顶点的四边形为平行四边形，请直接写出D′的坐标。

查看试题解析
22. 我市为加强学生的安全意识，组织了全市学生参加安全知识竞赛，为了解此次知识竞赛成绩的情况，随机抽取了部分参赛学生的成绩，整理并制作出如下的不完整的统计表和统计图，如图所示，请根据图表信息解答以下问题．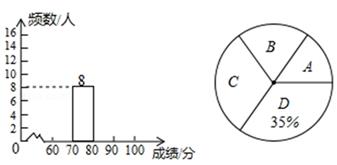

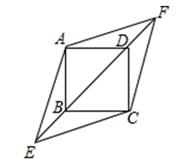
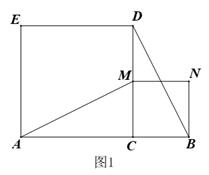
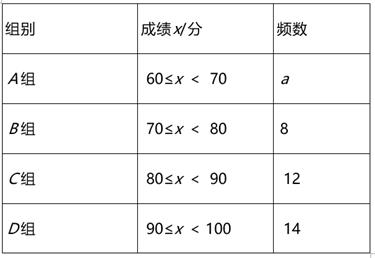(1)、一共抽取了个参赛学生的成绩；表中a＝；

(2)、补全频数分布直方图；

(3)、计算扇形统计图中“B”对应的圆心角度数；

(4)、若成绩在80分以上（包括80分）的为“优”等，则所抽取学生成绩为“优”的占所抽取学生的百分比是多少？

查看试题解析
23. 如图，已知矩形ABCD中，E是AD上的一点，F是AB上的一点，EF⊥EC，且EF＝EC，DE＝4cm，矩形ABCD的周长为36cm，求AE的长.

查看试题解析
24. 我校图书馆添置图书，用240元购进一种科普书，同时用200元购进一种文学书．由于科普书单价是文学书单价的1.5倍，因此学校所购买的文学书比科普书多4本．

(1)、求文学书的单价是多少？

(2)、学校买了文学书和科普书一共多少本？

查看试题解析
25. 如图所示，在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE＝DF，连接AE、AF、CE、CF.

(1)、求证：△ABE≌△ADF；

(2)、试判断四边形AECF的形状，并说明理由.

查看试题解析
26. 如图1，点C在线段AB上，分别以AC、BC为边在线段AB的同侧作正方形ACDE和正方形BCMN，连结AM、BD．

(1)、AM与BD的关系是：．

(2)、如果将正方形BCMN绕点C顺时针旋转锐角α，它不变（如图2）．（1）中所得的结论是否仍然成立？请说明理由．

(3)、在（2）的条件下，连接AB、DM，若AC＝4，BC＝2，求 $A B^{2} + D M^{2}$ 的值．

查看试题解析