湖北省十堰市2019届高三理数模拟考试试卷
试卷更新日期:2019-05-21 类型:高考模拟
一、单选题
-
1. 设复数 满足 ,其中 为虚数单位,则复数 对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 集合 , ,则 =( )A、 B、 C、 D、3. 设向量 , ,则与 垂直的向量的坐标可以是( )
A、 B、 C、 D、4. 直线 与 轴的交点为 ,点 把圆 的直径分为两段,则较长一段比上较短一段的值等于 ( )A、2 B、3 C、4 D、55. 某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队,平均分到甲、乙两个村进行义务巡诊,其中每个分队都必须有内科医生、外科医生和护士,则不同的分配方案有A、72种 B、36种 C、24种 D、18种6. 我国南北朝时期数学家、天文学家——祖暅,提出了著名的祖暅原理:“缘幂势即同,则积不容异也”.“幂”是截面积,“势”是几何体的高,意思是两等高几何体,若在每一等高处的截面积都相等,则两立方体体积相等.已知某不规则几何体与如图三视图所对应的几何体满足“幂势同”,则该不规则几何体的体积为( )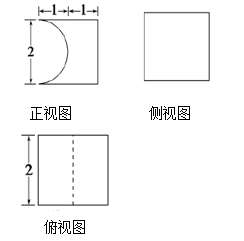 A、 B、 C、 D、7. 将函数 的图象向右平移 个单位长度得到 图像,则下列判断错误的是( )A、函数 在区间 上单调递增 B、 图像关于直线 对称 C、函数 在区间 上单调递减 D、 图像关于点 对称8. 如图是为了求出满足 的最小偶数 ,那么在
A、 B、 C、 D、7. 将函数 的图象向右平移 个单位长度得到 图像,则下列判断错误的是( )A、函数 在区间 上单调递增 B、 图像关于直线 对称 C、函数 在区间 上单调递减 D、 图像关于点 对称8. 如图是为了求出满足 的最小偶数 ,那么在 和
和  两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( ) 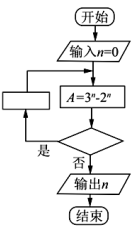 A、 和 B、 和 C、 和 D、 和9. 已知锐角 满足 ,则 ( )A、 B、 C、 D、10. 如图,圆M、圆N、圆P彼此相外切,且内切于正三角形ABC中,在正三角形ABC内随机取一点,则此点取自三角形MNP(阴影部分)的概率是( )
A、 和 B、 和 C、 和 D、 和9. 已知锐角 满足 ,则 ( )A、 B、 C、 D、10. 如图,圆M、圆N、圆P彼此相外切,且内切于正三角形ABC中,在正三角形ABC内随机取一点,则此点取自三角形MNP(阴影部分)的概率是( )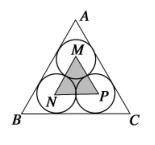 A、 B、 C、 D、11. 已知双曲线 的左,右焦点分别为 ,O为坐标原点,P为双曲线在第一象限上的点,直线PO, 分别交双曲线C的左,右支于另一点 ,且 ,则双曲线的离心率为( )A、 B、3 C、2 D、12. 设函数 ( ,e为自然对数的底数).定义在R上的函数 满足 ,且当 时, .若存在 ,且 为函数 的一个零点,则实数a的取值范围为( )A、 B、 C、 D、
A、 B、 C、 D、11. 已知双曲线 的左,右焦点分别为 ,O为坐标原点,P为双曲线在第一象限上的点,直线PO, 分别交双曲线C的左,右支于另一点 ,且 ,则双曲线的离心率为( )A、 B、3 C、2 D、12. 设函数 ( ,e为自然对数的底数).定义在R上的函数 满足 ,且当 时, .若存在 ,且 为函数 的一个零点,则实数a的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 在△ABC中,a=3, ,B=2A,则cosA= .14. 已知平面α,β,直线 .给出下列命题:
① 若 , ,则 ;② 若 , ,则 ;③ 若 ,则 ;④ 若 , ,则 .
其中是真命题的是 . (填写所有真命题的序号).
15. 甲、乙、丙、丁四位同学中仅有一人申请了北京大学的自主招生考试,当他们被问到谁申请了北京大学的自主招生考试时,甲说:“丙或丁申请了”;乙说:“丙申请了”;丙说:“甲和丁都没有申请”;丁说:“乙申请了”,如果这四位同学中只有两人说的是对的,那么申请了北京大学的自主招生考试的同学是 .16. 如图放置的边长为1的正方形 沿 轴滚动,点 恰好经过原点.设顶点 的轨迹方程是 ,则对函数 有下列判断:①函数 是偶函数;②对任意的 ,都有 ;③函数 在区间 上单调递减;④函数 的值域是 ;⑤ .其中判断正确的序号是 .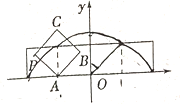
三、解答题
-
17. 已知数列 是递增的等差数列, ,且 是 与 的等比中项。(1)、求 ;(2)、若 ,求数列 的前 项和 。18. 某市有 四个景点,一位游客来该市游览,已知该游客游览 的概率为 ,游览 、 和 的概率都是 ,且该游客是否游览这四个景点相互独立.(1)、求该游客至多游览一个景点的概率;(2)、用随机变量 表示该游客游览的景点的个数,求 的概率分布和数学期望 .19. 如图(1),等腰梯形 , , , , 、 分别是 的两个三等分点.若把等腰梯形沿虚线 、 折起,使得点 和点 重合,记为点 ,如图(2).

(Ⅰ)求证:平面 平面 ;
(Ⅱ)求平面 与平面 所成锐二面角的余弦值.
20. 设椭圆 ( )的离心率为 ,圆 与 轴正半轴交于点 ,圆 在点 处的切线被椭圆 截得的弦长为 .(Ⅰ)求椭圆 的方程;
(Ⅱ)设圆 上任意一点 处的切线交椭圆 于点 ,试判断 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.