河南名校联盟2019届高三下学期理数2月联考试卷
试卷更新日期:2019-05-21 类型:高考模拟
一、单选题
-
1. 复数 ( 为虚数单位)等于( )A、 B、 C、 D、2. 已知集合 ,则 等于( )A、 B、 C、 D、3. 在区间 内,任取 个数 ,则满足 的概率为( )A、 B、 C、 D、4. 已知 ,则 ( )A、 B、 C、 D、5. 椭圆 的左、右焦点分别为 , ,上顶点为 ,若 的面积为 ,且 ,则椭圆方程为( )A、 B、 C、 D、6. 运行如图所示的程序框图,则输出 的值为( )
 A、 B、 C、 D、7. 榫卯(sǔnmǎo)是两个木构件上所采用的一种凹凸结合的连接方式.凸出部分叫榫,凹进去的部分叫卯,榫和卯咬合,起到连接作用.代表建筑有北京的紫禁城、天坛祈年殿,山西悬空寺等,如图是一种榫卯构件中榫的三视图,则该榫的表面积和体积为( )
A、 B、 C、 D、7. 榫卯(sǔnmǎo)是两个木构件上所采用的一种凹凸结合的连接方式.凸出部分叫榫,凹进去的部分叫卯,榫和卯咬合,起到连接作用.代表建筑有北京的紫禁城、天坛祈年殿,山西悬空寺等,如图是一种榫卯构件中榫的三视图,则该榫的表面积和体积为( )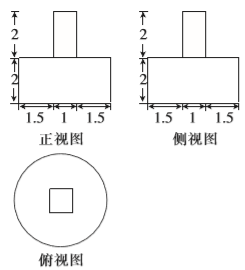 A、 B、 C、 D、8. 已知 满足约束条件 ,若目标函数 的最大值为 ,则实数 的值为( )A、 B、 C、 D、9. 在平面直角坐标系中,已知三点 为坐标原点.若向量 ,则 的最小值为( )A、 B、 C、 D、10. 设点 是正方体 的对角线 的中点,平面 过点 ,且与直线 垂直,平面 平面 ,则 与 所成角的余弦值为( )A、 B、 C、 D、11. 已知函数 的一个零点是 是 的图象的一条对称轴,则 取最小值时, 的单调增区间是( )A、 B、 C、 D、12. 设实数 ,且不等式 对 恒成立,则 的最大值是()A、 B、 C、 D、
A、 B、 C、 D、8. 已知 满足约束条件 ,若目标函数 的最大值为 ,则实数 的值为( )A、 B、 C、 D、9. 在平面直角坐标系中,已知三点 为坐标原点.若向量 ,则 的最小值为( )A、 B、 C、 D、10. 设点 是正方体 的对角线 的中点,平面 过点 ,且与直线 垂直,平面 平面 ,则 与 所成角的余弦值为( )A、 B、 C、 D、11. 已知函数 的一个零点是 是 的图象的一条对称轴,则 取最小值时, 的单调增区间是( )A、 B、 C、 D、12. 设实数 ,且不等式 对 恒成立,则 的最大值是()A、 B、 C、 D、二、填空题
-
13. (x+1)2(x-2)5的展开式中含 x3 项的系数为 .
14. 已知函数 若 存在 个零点,则 的取值范围是 .15. 已知双曲线 的离心率为 ,若点 与点 都在双曲线 上,则该双曲线的焦点到其一条渐近线的距离为 .16. 在 中,角 , , 的对边分别为 , , ,若 , 是锐角,且 , ,则 的面积为 .三、解答题
-
17. 已知等比数列 是递增数列,其公比为 ,前 项和为 ,并且满足 , 是 和 的等差中项.
(Ⅰ)求数列 的通项公式;
(Ⅱ)若 , ,求使 成立的正整数 的值.
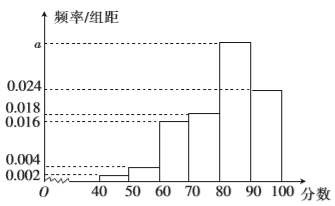
18. 某市的教育主管部门对所管辖的学校进行年终监督评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的同学中随机抽取若干师生,进行评分(满分 分),绘制如下频率分布直方图(分组区间为 ),并将分数从低到高分为四个等级:满意度评分
满意度等级
不满意
基本满意
满意
非常满意
已知满意度等级为基本满意的有 人.
(Ⅰ)求频率分布直方图中 的值及不满意的人数;
(Ⅱ)在等级为不满意的师生中,老师占 ,现从等级的师生中按分层抽样的方法抽取 人了解不满意的原因,并从这 人中抽取 人担任整改督导员,记 为整改督导员中老师的人数,求 的分布列及数学期望.
 19. 如图,在四棱锥 中 ,且 和 分别是棱 和 的中点.
19. 如图,在四棱锥 中 ,且 和 分别是棱 和 的中点.
(Ⅰ)求证: ;
(Ⅱ)求直线 与平面 所成的角的正弦值.
20. 已知 ,抛物线 : 与抛物线 : 异于原点 的交点为 ,且抛物线 在 处的切线与 轴交于点 ,抛物线 在点 处的切线与 轴交于点 ,与 轴交于点 .(Ⅰ)若直线 与抛物线 交于点 , ,且 ,求 的值;
(Ⅱ)证明: 的面积与四边形 的面积之比为定值.