湖南省邵阳市普通高中2019年数学学业水平模拟考试试卷
试卷更新日期：2019-05-21 类型：高考模拟
一、选择题：本大题共10小题，每小题4分，共40分。
-
1. 如图，一个几何体的三视图都是半径为1的圆，则该几何体是（ ）
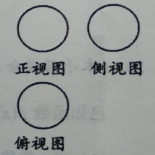A、圆柱 B、圆锥 C、圆台 D、球2. 已知集合A={-1，0，2}，B={x，3}，若A∩B={-1}，则x的值为（ ）A、3 B、2 C、0 D、-13. 执行如图所示的程序框图，若输入x的值为2，则输出的y值为（ ）
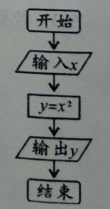A、2 B、3 C、4 D、54. 函数y=sinx，x∈R的最小正周期是（ ）A、1 B、2 C、π D、2π5. 下列函数中，在区间（0，+∞）上为减函数的是（ ）A、y=( )x B、y=log2x C、y=x2 D、y=cosx6. 在长度为6的线段AB上任取一点C，则AC之间的距离小于2的概率为（ ）A、 B、 C、 D、7. 如图，在△ABC中， =（ ）
A、 B、 C、0 D、8. 已知直线l过点（2，0），且与直线y=-2x+1平行，则直线/的方程为（ ）A、y=2x-4 B、y=2x+4 C、y=-2x+4 D、y=-2x-49. 如图，在△ABC中，AB=2，AC=1，∠A=120°，则BC长为（ ）
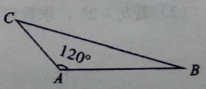A、 B、 C、 D、10. 实数x，y满足不等式组 则z=x-y的最大值为（ ）A、2 B、1 C、-2 D、-1二、填空题：本大题共5小题，每小题4分，共20分。
-
11. 已知sinθ=cosθ，则tanθ的值为。12. 不等式x（x-1）<0的解集为。13. 已知x0是函数f（x）=2x-4的零点，则实数x0的值为。14. 为调查学校新生的运动时间，该收有学生1800人，教师200人，现用分层指样的方法抽取20人作样本，则从教师中应抽取人.
15. 已知直线l：3x-4y+6=0，圆C：（x-1）2+（y-1）2=P（G>0），若直线l与圆C相切，则圆C的半径r=.三、解答题：本大题共5小题，共40分。
-
16. 已知等差数列{an}的首项为1，且a2+a3=5.(1)、求公差d及an；(2)、若bn=2an ， 求数列{bn}的前项和Sn。17. 如图，在四棱锥P-ABCD中，底面ABCD是正方形，PAL底面ABCD，且PA=AB.
(1)、求证：BD⊥平面PAC；(2)、求异面直线BC与PD所成的角.18. 已知向量a=（1，sinx），b=（1，2cosx），函数f（x）=a-b(1)、求f( )的值：(2)、求f（x）的最大值及取得最大值时x的集合。19. 为了解某校高二学生的学业水平，现从某次数学模拟测试中随机抽取10名学生的成绩进行分析，得到如图的频率分布直方图。
(1)、若成绩不低于80分为优秀，根据频率分布直方图中的数据，估算该校这次数学模拟测试的优秀率；(2)、从样本低于80分的学生中任取2人，求选出的2人成绩均在70分以下的概率。20. 已知函数f（x）=logax（a>0，且a≠1），且f（2）=1(1)、求a的值，并写出函数f（x）的定义域；(2)、设g（x）=f（2-x）-f（2+x），判断g（x）的奇偶性，并说明理由：(3)、若不等式f(t·9x）≥f(3x-t)对任意x∈[1，2]恒成立，求实数t的取值范围。