黑龙江省哈尔滨市巴彦县2018-2019学年中考数学二模试卷
试卷更新日期:2019-05-20 类型:中考模拟
一、选择题(满分30分)
-
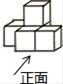
1. ﹣2019的倒数是( )A、2019 B、 C、 D、﹣20192. 下列运算中,正确的是( )A、3a2﹣a2=2 B、(2a2)2=2a4 C、a6÷a3=a2 D、a3•a2=a53. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、等边三角形 B、正六边形 C、正方形 D、圆4. 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
 A、
A、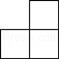 B、
B、 C、
C、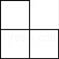 D、
D、 5. 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( )
5. 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( ) A、2 B、4 C、4 D、86. 若要得到函数y=(x+1)2+2的图象,只需将函数y=x2的图象( )A、先向右平移1个单位长度,再向上平移2个单位长度 B、先向左平移1个单位长度,再向上平移2个单位长度 C、先向左平移1个单位长度,再向下平移2个单位长度 D、先向右平移1个单位长度,再向下平移2个单位长度7. 解分式方程 ﹣3= 时,去分母可得( )A、1﹣3(x﹣2)=4 B、1﹣3(x﹣2)=﹣4 C、﹣1﹣3(2﹣x)=﹣4 D、1﹣3(2﹣x)=48. 对于反比例函数 ,下列说法正确的是( )A、图象经过点(2,﹣1) B、图象位于第二、四象限 C、图象是中心对称图形 D、当x<0时,y随x的增大而增大9. 如图,在▱ABCD中,点E在AD边上,CE、BA的延长线交于点F,下列结论错误的是( )
A、2 B、4 C、4 D、86. 若要得到函数y=(x+1)2+2的图象,只需将函数y=x2的图象( )A、先向右平移1个单位长度,再向上平移2个单位长度 B、先向左平移1个单位长度,再向上平移2个单位长度 C、先向左平移1个单位长度,再向下平移2个单位长度 D、先向右平移1个单位长度,再向下平移2个单位长度7. 解分式方程 ﹣3= 时,去分母可得( )A、1﹣3(x﹣2)=4 B、1﹣3(x﹣2)=﹣4 C、﹣1﹣3(2﹣x)=﹣4 D、1﹣3(2﹣x)=48. 对于反比例函数 ,下列说法正确的是( )A、图象经过点(2,﹣1) B、图象位于第二、四象限 C、图象是中心对称图形 D、当x<0时,y随x的增大而增大9. 如图,在▱ABCD中,点E在AD边上,CE、BA的延长线交于点F,下列结论错误的是( ) A、 = B、 C、 D、10. 如果方程x2﹣8x+15=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为( )A、 B、 C、 D、 或
A、 = B、 C、 D、10. 如果方程x2﹣8x+15=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为( )A、 B、 C、 D、 或二、填空题(满分30分)
-
11. 58万千米用科学记数法表示为:千米.12. 计算 ﹣9 的结果是 .13. 函数y= 的自变量x的取值范围是 .14. 分解因式:3x2﹣3y2= .15. 已知关于x的不等式组 无解,则a的取值范围是 .16. 抛物线y=2(x+3)2+4与y轴交点坐标为 .17. 一个扇形所在圆的半径为a,它的弧所对的圆心角为120°,那么这个扇形的面积为(结果保留π).18. 李老师想从小明、小红、小丽和小亮四个人中用抽签的方式抽取两个人做流动值周生,则小红和小丽同时被抽中的概率是 .
19. 如图,在直角坐标系中,点A的坐标是(2,0),点B的坐标是(0,3),以AB为腰作等腰三角形,则另一顶点在坐标轴上的有个。 20. 如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠B,AB=2AE,若△ADE的面积为2,则四边形BCED的面积为 .
20. 如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠B,AB=2AE,若△ADE的面积为2,则四边形BCED的面积为 .
三、解答题(满分60分)
-
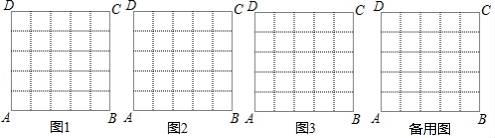
21. 先化简,再求代数式 ÷(x﹣3﹣ )的值,其中x=3tan45°+2cos30°.22. 在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.请你画出三个不同的直角三角形,并直接在网格下方写出其周长.
 23. 某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个),该校从八年级学生中随机抽取了若干名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图.
23. 某学校准备组织八年级学生春游,供学生选择的春游地点分别是:植物园、太阳岛、东北虎林园.每名学生只能选择其中一个春游地点(必选且只选一个),该校从八年级学生中随机抽取了若干名学生,对他们选择春游地点的情况进行调查,并根据调查结果绘制成如图所示的条形统计图. (1)、求此次抽取的学生人数;(2)、求此次抽取的学生中选择去植物园春游的人数占所抽取人数的百分比是多少?(3)、如果该校八年级有540名学生,请你估计选择去太阳岛春游的学生有多少名?24. 把一张矩形纸片ABCD按如图方式折叠,使顶点B落在边AD上(记为点B′),点A落在点A′处,折痕分别与边AD、BC交于点E、F.
(1)、求此次抽取的学生人数;(2)、求此次抽取的学生中选择去植物园春游的人数占所抽取人数的百分比是多少?(3)、如果该校八年级有540名学生,请你估计选择去太阳岛春游的学生有多少名?24. 把一张矩形纸片ABCD按如图方式折叠,使顶点B落在边AD上(记为点B′),点A落在点A′处,折痕分别与边AD、BC交于点E、F.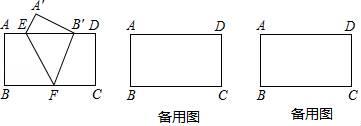 (1)、试在图中连接BE,求证:四边形BFB′E是菱形;(2)、若AB=9,BC=27,求线段BF长能取到的整数值;并求出线段BF取到最大整数时,折痕EF的长.25. 目前节能灯已基本普及,节能还环保,销量非常好,某商场计划购进甲、乙两种型号节能灯共1200只,这两种节能灯的进价、售价如表所示:
(1)、试在图中连接BE,求证:四边形BFB′E是菱形;(2)、若AB=9,BC=27,求线段BF长能取到的整数值;并求出线段BF取到最大整数时,折痕EF的长.25. 目前节能灯已基本普及,节能还环保,销量非常好,某商场计划购进甲、乙两种型号节能灯共1200只,这两种节能灯的进价、售价如表所示:进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)、商场应如何进货,使进货款恰好为46000元?(2)、若商场销售完节能灯后获利不超过进货价的30%,至少购进甲种型号节能灯多少只?26. 已知:在△MAB中,C、D分别为BM、AM上的点,四边形ABCD内接于⊙O,连接AC,∠MCD=∠ACD; (1)、如图①,求证:弧AD=弧BD;(2)、如图②,若AB为直径,CD= BC,求tan∠DAC值;(3)、如图③,在(2)的条件下,E为弧CD上一点(不与C、D重合),F为AB上一点,连接EF交AC于点N,连接DN、DE,若DN=DE,AB=10,∠ABC﹣45°=∠ANF,求AN的长.27. 如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.
(1)、如图①,求证:弧AD=弧BD;(2)、如图②,若AB为直径,CD= BC,求tan∠DAC值;(3)、如图③,在(2)的条件下,E为弧CD上一点(不与C、D重合),F为AB上一点,连接EF交AC于点N,连接DN、DE,若DN=DE,AB=10,∠ABC﹣45°=∠ANF,求AN的长.27. 如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B. (1)、线段AB,BC,AC的长分别为AB= , BC= , AC=;(2)、折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
(1)、线段AB,BC,AC的长分别为AB= , BC= , AC=;(2)、折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.请从下列A、B两题中任选一题作答,我选择哪个题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.