湖南省新宁县二中2019届高二数学学业水平模拟考试试卷

试卷更新日期：2019-05-20 类型：高考模拟

进入出卷网下载

一、选择题：本大题共10小题，每小题4分，满分40分。

1. 如图所示，该正三棱柱的俯视图是（）

A、 B、 C、 D、

查看试题解析
2. 已知集合M={1，2}，N={2，3}，则M∩N中元素的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
3. 已知x与y之间的一组数据：

x

1

2

3

4

y

3

5

7

9

则y与x的线性回归方程y=bx+a必过点（）

A、(2，6） B、(2.5，6） C、(3，8) D、(3.5，8)

查看试题解析
4. 化简：(sin a-cos a）²=（）

A、1+sin 2a B、1-sina C、1-sin2a D、1+sina

查看试题解析
5. 已知定义在R上的函数f(x)的图像是连续不断的，且有如下对应值表：

x

1

2

3

f(x)

6.1

2.9

-3.5

那么函数f(x)一定存在零点的区间是（）

A、（-∞，1） B、（1，2） C、（2，3） D、（3，+∞)

查看试题解析
6. 已知角a的终边经过点P（-3，-4)，则下列结论中正确的是（）

A、tana=- $\frac{4}{3}$ B、sina=- $\frac{3}{5}$ C、cosa=- $\frac{4}{5}$ D、tana= $\frac{4}{3}$

查看试题解析
7. 阅读下边的流程图，若输入的x=2，则输出的结果是（）

A、4 B、5 C、6 D、7

查看试题解析
8. 在△ABC中，角A，B，C所对的边分别为a．b．c，若A=60°，a= $\sqrt{3}$ ，b= $\sqrt{2}$ ，则B=（）

A、30° B、45° C、135° D、45°或135°

查看试题解析
9. 若实数x，y满足 ${\begin{cases} x - y + 1 \geq 0 \\ x + y \geq 0 \\ x \leq 0 \end{cases}$ ，则z=x-2y的最小值为（）

A、-2 B、- $\frac{3}{2}$ C、-1 D、0

查看试题解析
10. 由直线y=x+1上的一点向圆（x-3）²+y²=1引切线，则切线长的最小值为（）

A、1 B、 $\sqrt{7}$ C、2 $\sqrt{2}$ D、3

查看试题解析

二、填空题：本大题共5小题，每小题4分，满分20分。

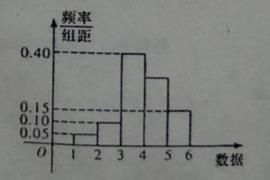
11. 某个容量为100的样本的频率分布直方图如下，则在区间[4，5]上的数据的频数为。

查看试题解析
12. 已知△ABC是边长为2的等边三角形， $\vec{A B} \cdot \vec{A C}$ =

查看试题解析
13. 若x>0，则2x+ $\frac{1}{x}$ 的最小值为．

查看试题解析
14. 已知直线l₁:y=3x+1,l₂:kx-2y-3=0，若l₁∥l₂,则k= ．

查看试题解析
15. 设 $g (x) = {\begin{cases} e^{x}, x \leq 0 \\ 1 n x, x > 0 \end{cases}$ ,则g（g（-1））= ．

查看试题解析

三、解答题：本大题共5小题，满分40分。

16. 学校举行班级篮球赛，某运动员每场比赛得分记录的茎叶图如图所示。

(1)、求该运动员得分的中位数和平均数；

(2)、估计该运动员每场得分超过10分的概率。

查看试题解析
17. 已知函数f(x)=sin x+ $\sqrt{3}$ cosx．

(1)、求函数f(x)的最小正周期；

(2)、将函数f（x）的图像上所有的点向右平移 $\frac{π}{3}$ 个单位，得到函数g（x）的图像，写出g（x）的解析式，并求g（x）在x∈（0，π）上的单调递增区间．

查看试题解析
18. 如图，四边形ABCD为正方形，PD⊥平面ABCD，E、F分别为BC和PC的中点

(1)、求证：EF∥平面PBD．

(2)、如果AB=PD，求异面直线EF与BD所成角的正切值

查看试题解析
19. 在等差数列{a_m}中，已知a₂=2，a₄=4．

(1)、求数列{am}的通项公式a_m；

(2)、设b_m=2^am，求数列{b_m}前5项的和S₅ ．

查看试题解析
20. 已知二次函数f（x）=ax²+bx+c（a≠0)，f(-2)=f（0）=0．f（-1）=-1

(1)、求函数f(x)的解析式；

(2)、设g（x）=f（-x)- λf(x)+1,若g（x）在[-1，1]上是减函数，求实数λ的取值范围．

查看试题解析

x	1	2	3
f(x)	6.1	2.9	-3.5