新疆乌鲁木齐地区2019届高三理数第二次质量监测试卷

试卷更新日期：2019-05-17 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $A = {x | x < 1}$ ， $B = {x | x^{2} < 4}$ ，则 $A \cap^{} B$ 等于 $($ $)$

A、 ${x | - 2 < x < 1}$ B、 ${x | 1 < x < 2}$ C、 ${x | - 1 < x < 2}$ D、 ${x | x < 2}$

查看试题解析
2. 已知复数z= $\frac{2 - i}{1 + i}$ （i是虚数单位），则复数z的虚部为（）

A、 $- \frac{3}{2}$ B、 $- \frac{3}{2} i$ C、 $\frac{1}{2}$ D、 $\frac{1}{2} i$

查看试题解析
3. 图象关于原点对称且在定义域内单调递增的函数是（）

A、 $f (x) = cos x - 1$ B、 $f (x) = x^{2} + 2$ C、 $f (x) = - \frac{1}{x}$ D、 $f (x) = x^{3}$

查看试题解析
4. 若实数x，y满足 ${\begin{matrix} x - 4 y + 3 \leq 0 \\ 3 x + 5 y - 25 \leq 0 \\ x \geq 1 \end{matrix}$ ，则函数 $z = 2 x + y$ 的最大值为 $($ $)$

A、12 B、 $\frac{32}{5}$ C、3 D、15

查看试题解析
5. 我国南北朝时期数学家、天文学家祖暅提出了著名的祖暅原理：“幂势既同，则积不容异” $.$ 其中“幂”即是截面积，“势”是几何体的高，意思是两等高立方体，若在每一等高处的截面积都相等，则两立方体的体积相等，已知某不规则几何体与如图所示的几何体满足“幂势同”，则该不规则几何体的体积为 $($ $)$

A、 $4 - \frac{π}{2}$ B、 $8 - π$ C、 $8 - \frac{4 π}{3}$ ． $8 - 2 π$

查看试题解析
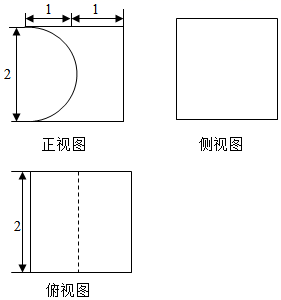6. 已知实数 $a = 2^{ln 2}$ ， $b = 2 + 2 ln 2$ ， $c = {(ln 2)}^{2}$ ，则a，b，c的大小关系是 $($ $)$

A、 $c < a < b$ B、 $c < b < a$ C、 $b < a < c$ D、 $a < c < b$

查看试题解析
7. 如图所示算法框图，当输入的 $x$ 为1时，输出的结果为（）

A、3 B、4 C、5 D、6

查看试题解析
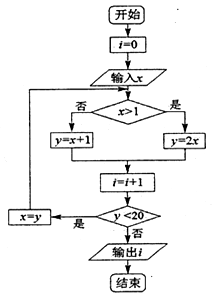8. 已知 $F_{1}$ ， $F_{2}$ 是双曲线 $x^{2} - y^{2} = 1$ 的焦点，以 $F_{1} F_{2}$ 为直径的圆与一条渐近线交于P，Q两点，则 $△ F_{1} P Q$ 的面积为 $($ $)$

A、 $\frac{\sqrt{2}}{2}$ B、1 C、 $\sqrt{2}$ D、2

查看试题解析
9. 若关于x的方程 ${(sin x + cos x)}^{2} + cos 2 x = m$ 在区间 $[0 ， π)$ 上有两个根 $x_{1}$ ， $x_{2}$ ，且 $| x_{1} - x_{2} | \geq \frac{π}{4}$ ，则实数m的取值范围是 $($ $)$

A、 $[0 ， 2)$ B、 $[0 ， 2]$ C、 $[1 ， \sqrt{2} + 1]$ D、 $[1 ， \sqrt{2} + 1)$

查看试题解析
10. 设 $F_{1}$ ， $F_{2}$ 分别是椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点，直线l过 $F_{1}$ 交椭圆C于A，B两点，交y轴于C点，若满足 $\vec{F_{1} C} = \frac{3}{2} \vec{A F_{1}}$ 且 $∠ C F_{1} F_{2} = 30^{\circ}$ ，则椭圆的离心率为 $($ $)$

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
11. 已知A，B，C为球O的球面上的三个定点， $∠ A B C = 60^{\circ}$ ， $A C = 2$ ，P为球O的球面上的动点，记三棱锥p一ABC的体积为 $V_{1}$ ，三棱銋O一ABC的体积为 $V_{2}$ ，若 $\frac{V_{1}}{V_{2}}$ 的最大值为3，则球O的表面积为 $($ $)$

A、 $\frac{16 π}{9}$ B、 $\frac{64 π}{9}$ C、 $\frac{3 π}{2}$ D、 $6 π$

查看试题解析
12. f（x）的定义域是（0，+∞），其导函数为f′（x），若f′（x）- $\frac{f (x)}{x}$ =1-lnx，且f（e）=e²（其中e是自然对数的底数），则（）

A、 $f (2) < 2 f (1)$ B、 $4 f (3) < 3 f (4)$ C、当 $x > 0$ 时， $f (x) > 0$ D、当 $x > 0$ 时， $f (x) - e x \leq 0$

查看试题解析

二、填空题

13. 若 $s i n (\frac{π}{6} - α) = \frac{1}{4}$ ，则 $cos (2 α - \frac{π}{3})$ 的值为．

查看试题解析
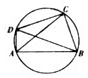
14. 在平面直角坐标系xOy中，若直线 $y = x + m$ 与曲线 $y = a sin x + b cos x (a ，$ b， $m \in R)$ 相切于点 $(0 ， 1)$ ，则 $\frac{a + b}{m}$ 的值为．

查看试题解析
15. 如图，在圆内接四边形ABCD中，已知对角线BD为圆的直径， $A B = A C = 2 \sqrt{2}$ ， $A D = 1.$ 则 $\vec{A C} \cdot \vec{B D}$ 的值为．

查看试题解析

三、解答题

16. 记公差不为零的等差数列{a_n}的前n项和为S_n ，已知a₁=2，a₄是a₂与a₈的等比中项．
（Ⅰ）求数列{a_n}的通项公式；

（Ⅱ）求数列{ $\frac{1}{S_{n}}$ }的前n项和T_n ．

查看试题解析
17. 如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠DAB=60°，PD=4，M为PD的中点，E为AM的中点，点F在线段PB上，且PF=3FB．

（Ⅰ）求证EF∥平面ABCD；

（Ⅱ）若平面PDC⊥底面ABCD，且PD⊥DC，求平面PAD与平面PBC所成锐二面角的余弦值．

查看试题解析

18. 某互联网公司为了确定下一季度的前期广告投入计划，收集了近

6

个月广告投入量

x

（单位：万元）和收益

y

（单位：万元）的数据如下表：

月份	$1$	$2$	$3$	$4$	$5$	$6$
广告投入量	$2$	$4$	$6$	$8$	$10$	$12$
收益	$14.21$	$20.31$	$31.8$	$31.18$	$37.83$	$44.67$

他们分别用两种模型① $y = b x + a$ ，② $y = a e^{b x}$ 分别进行拟合，得到相应的回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值：

$\bar{x}$	$\bar{y}$	$\sum_{i = 1}^{6} x_{i} y_{i}$	$\sum_{i = 1}^{6} x_{i}^{2}$
$7$	$30$	$1464.24$	$364$

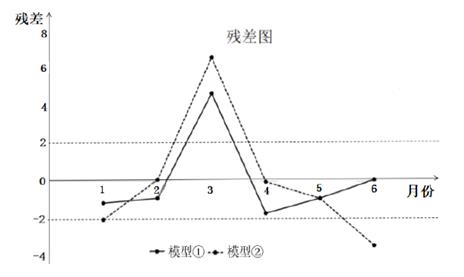
（Ⅰ）根据残差图，比较模型①，②的拟合效果，应选择哪个模型？并说明理由；

（Ⅱ）残差绝对值大于 $2$ 的数据被认为是异常数据，需要剔除：

（ⅰ）剔除异常数据后求出（Ⅰ）中所选模型的回归方程；

（ⅱ）若广告投入量 $x = 18$ 时，该模型收益的预报值是多少？

附：对于一组数据 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ，……， $(x_{n} ， y_{n})$ ，其回归直线 $\hat{y} = \hat{b} x + \hat{a}$ 的斜率和截距的最小二乘估计分别为：

 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ $= \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ .

查看试题解析

19. 已知拋物线C： $x^{2} = 2 p y$ 经过点 $P (2, 1)$ ，其焦点为F，M为抛物线上除了原点外的任一点，过M的直线l与x轴、y轴分别交于A，B两点．
$($ Ⅰ $)$ 求抛物线C的方程以及焦点坐标；

$($ Ⅱ $)$ 若 $△ A M F$ 与 $△ A B F$ 的面积相等，证明直线l与抛物线C相切．

查看试题解析
20. 已知函数f（x）=e^x+ $\frac{x}{t x - 1}$ （其中e是自然对数的底数）．
（Ⅰ）当t=0时，求f（x）的最值；

（Ⅱ）若t≠0时，f（x）在（ $\frac{1}{t} ， + \infty$ ）上的最小值为1，求实数t的取值范围．

查看试题解析
21. 在平面直角坐标系xOy中，曲线 $C_{1}$ 的参数方程为 ${\begin{matrix} x = t \\ y = 3 - t \end{matrix}$ ， $(t$ 为参数 $)$ ，在以坐标原点为极点，x轴非负半轴为极轴的极坐标系中，曲线 $C_{2}$ 的极坐标方程为 $ρ = 4 sin θ$ ．
$($ Ⅰ $)$ 写出 $C_{1}$ 的普通方程和 $C_{2}$ 的直角坐标方程；

$($ Ⅱ $)$ 若 $C_{1}$ 与 $C_{2}$ 相交于A，B两点，求 $△ O A B$ 的面积．

查看试题解析
22. 已知函数 $f (x) = 2 | x + 1 | - | x - a |$ ， $a \in R$ ．
$($ Ⅰ $)$ 当 $a = 1$ 时，求不等式 $f (x) < 0$ 的解集；

$($ Ⅱ $)$ 若关于x的不等式 $f (x) < x$ 有实数解，求实数a的取值范围．

查看试题解析