2016-2017学年四川省成都市九校联考高二下学期期中数学试卷（理科）

试卷更新日期：2017-05-19 类型：期中考试

进入出卷网下载

一、选择题

1. 直三棱柱ABC﹣A₁B₁C₁中，若 $\vec{C A}$ = $\vec{a}$ ， $\vec{C B}$ = $\vec{b}$ ， $\vec{C C_{1}}$ = $\vec{c}$ ，则 $\vec{A_{1} B}$ =（）

A、 $\vec{a}$ + $\vec{b}$ ﹣ $\vec{c}$ B、 $\vec{a}$ ﹣ $\vec{b}$ + $\vec{c}$ C、﹣ $\vec{a}$ + $\vec{b}$ + $\vec{c}$ D、﹣ $\vec{a}$ + $\vec{b}$ ﹣ $\vec{c}$

查看试题解析
2. 函数 f （ x）=sin x+e^x ，则 f'（0）的值为（）

A、1 B、2 C、3 D、0

查看试题解析
3. 已知m，n表示两条不同直线，α表示平面，下列说法正确的是（　　）

A、若m∥α，n∥α，则m∥n B、若m⊥α，n⊂α，则m⊥n C、若m⊥α，m⊥n，则n∥α D、若m∥α，m⊥n，则n⊥α

查看试题解析
4. 函数f（x）= $\frac{x}{\ln x}$ 的单调递减区间是（）

A、（0，e） B、（0，1），（1，e） C、（e，+∞） D、（﹣∞，e）

查看试题解析
5. 如图，在棱长为2的正方体ABCD﹣A₁B₁C₁D₁中，O是底面ABCD的中心，E、F分别是CC₁、AD的中点，那么异面直线OE和FD₁所成的角的余弦值等于（）

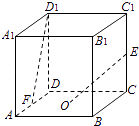A、 $\frac{\sqrt{10}}{5}$ B、 $\frac{\sqrt{15}}{5}$ C、 $\frac{4}{5}$ D、 $\frac{2}{3}$

查看试题解析
6. 已知函数f（x）=x﹣sinx，若x₁、 $x_{2} \in [- \frac{π}{2} ， \frac{π}{2}]$ 且f（x₁）+f（x₂）＞0，则下列不等式中正确的是（）

A、x₁＞x₂ B、x₁＜x₂ C、x₁+x₂＞0 D、x₁+x₂＜0

查看试题解析
7. 某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x的值是（）

A、2 B、 $\frac{9}{2}$ C、 $\frac{3}{2}$ D、3

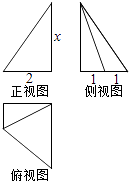查看试题解析
8. 若对任意的x＞0，恒有lnx≤px﹣1（p＞0），则p的取值范围是（）

A、（0，1] B、（1，+∞） C、（0，1） D、[1，+∞）

查看试题解析
9. 甲、乙两人约定在下午 4：30：5：00 间在某地相见，且他们在 4：30：5：00 之间到达的时刻是等可能的，约好当其中一人先到后一定要等另一人 20 分钟，若另一人仍不到则可以离去，则这两人能相见的概率是（）

A、 $\frac{3}{4}$ B、 $\frac{8}{9}$ C、 $\frac{7}{16}$ D、 $\frac{11}{12}$

查看试题解析
10. 如图在一个60° 的二面角的棱上有两个点A，B，线段分别AC、BD在这个二面角的两个面内，并且都垂直于棱AB，且AB=AC=a，BD=2a，则CD 的长为（）

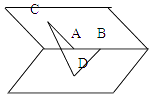A、2a B、 $\sqrt{5}$ a C、a D、 $\sqrt{3}$ a

查看试题解析
11. 已知函数f （ x）=ax³+bx²+cx+d 的图象如图所示，则 $\frac{b + 1}{a + 1}$ 的取值范围是（）

A、（﹣ $\frac{3}{2}$ ， $\frac{1}{2}$ ） B、（﹣ $\frac{2}{5}$ ，1） C、（﹣ $\frac{1}{2}$ ， $\frac{3}{2}$ ） D、（﹣ $\frac{3}{2}$ ，1）

查看试题解析
12. 已知F₁ ， F₂分别为双曲线C： $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1的左、右焦点，若存在过F₁的直线分别交双曲线C的左、右支于A，B两点，使得∠BAF₂=∠BF₂F₁ ，则双曲线C的离心率e的取值范围是（）

A、（3，+∞） B、（1，2+ $\sqrt{5}$ ） C、（3，2+ $\sqrt{5}$ ） D、（1，3）

查看试题解析

二、填空题

13. $\int_{0}^{1}$ x²dx= ．

查看试题解析
14. 已知椭圆 C₁： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）与双曲线 C₂：x²﹣y²=4 有相同的右焦点F₂ ，点P是C₁与C₂的一个公共点，若|PF₂|=2，则椭圆 C₁的离心率等于．

查看试题解析
15. 四棱柱 ABCD﹣A₁B₁C₁D₁中，底面为平行四边形，以顶点 A 为端点的三条棱长都相等，且两两夹角为 60°．则线段 AC₁与平面ABC所成角的正弦值为．

查看试题解析
16. 已知函数 $f (x) = 1 - \frac{m e^{x}}{x^{2} + x + 1}$ ，若存在唯一的正整数x₀ ，使得f（x₀）≥0，则实数m的取值范围为．

查看试题解析

三、解答题

17. 如图，在直三棱柱ABC﹣A₁B₁C₁中，AC⊥BC，点D是AB的中点．求证：

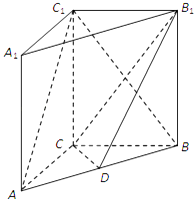(1)、AC⊥BC₁；

(2)、AC₁∥平面B₁CD．

查看试题解析
18. 某校举行环保知识竞赛，为了了解本次竞赛成绩情况，从得分不低于50分的试卷中随机抽取100名学生的成绩（得分均为正数，满分100分），进行统计，请根据频率分布表中所提供的数据，解答下列问题：
（Ⅰ）求a、b的值；
（Ⅱ）若从成绩较好的第3、4、5组中，按分层抽样的方法抽取6人参加社区志愿者活动，并从中选出2人做负责人，求2人中至少有1人是第四组的概率．
组号
分组
频数
频率
第1组
[50，60]
5
0.05
第2组
[60，70]
a
0.35
第3组
[70，80]
30
b
第4组
[80，90]
20
0.20
第5组
[90，100]
10
0.10
合计
100
1.00

查看试题解析
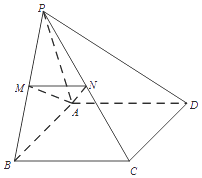
19. 已知函数f（x）=x²+2alnx．

(1)、若函数f（x）的图象在（2，f（2））处的切线斜率为1，求实数a的值；

(2)、求函数f（x）的单调区间；

(3)、若函数 $g (x) = \frac{2}{x} + f (x)$ 在[1，2]上是减函数，求实数a的取值范围．

查看试题解析
20. 在四棱锥P﹣ABCD中，△PAB为正三角形，四边形ABCD为矩形，平面PAB⊥平面ABCD，AB=2AD，M，N分别为PB，PC中点．
（Ⅰ）求证：MN∥平面PAD；
（Ⅱ）求二面角B﹣AM﹣C的大小；
（Ⅲ）在BC上是否存在点E，使得EN⊥平面AMN？若存在，求 $\frac{B E}{B C}$ 的值；若不存在，请说明理由．

查看试题解析
21. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0 ）经过点 P（1， $\frac{\sqrt{3}}{2}$ ），离心率 e= $\frac{\sqrt{3}}{2}$

（Ⅰ）求椭圆C的标准方程．
（Ⅱ）设过点E（0，﹣2 ）的直线l 与C相交于P，Q两点，求△OPQ 面积的最大值．

查看试题解析
22. 已知f （ x）= $\frac{1}{2}$ x² ， g （ x）=a ln x（a＞0）．
（Ⅰ）求函数 F （ x）=f（x）g（x）的极值
（Ⅱ）若函数 G（ x）=f（x）﹣g（x）+（a﹣1）在区间（ $\frac{1}{e}$ ，e）内有两个零点，求的取值范围；
（Ⅲ）函数 h（ x）=g （ x ）﹣x+ $\frac{1}{x}$ ，设 x₁∈（0，1），x₂∈（1，+∞），若 h（ x ₂）﹣h（ x ₁）存在最大值，记为 M （a），则当 a≤e+1 $\frac{1}{e}$ 时，M （a）是否存在最大值？若存在，求出其最大值；若不存在，请说明理由．

查看试题解析

组号	分组	频数	频率
第1组	[50，60]	5	0.05
第2组	[60，70]	a	0.35
第3组	[70，80]	30	b
第4组	[80，90]	20	0.20
第5组	[90，100]	10	0.10
合计		100	1.00