2016-2017学年山东省潍坊市寿光市高二下学期期中数学试卷（理科）

试卷更新日期：2017-05-19 类型：期中考试

进入出卷网下载

一、选择题：

1. 在导数定义中“当△x→0时， $\frac{Δ y}{Δ x}$ →f′（x₀）”中的，△x的取值为（）

A、正值 B、负值 C、正值、负值或零 D、正值或负值，但不能为零

查看试题解析
2. 设A，B为相互独立事件，下列命题中正确的是（）

A、A与B是对立事件 B、A与B是互斥事件 C、A与 $\bar{B}$ 是相互独立事件 D、 $\bar{A}$ 与 $\bar{B}$ 不相互独立

查看试题解析
3. 下列求导结果正确的是（）

A、（a﹣x²）′=1﹣2x B、（2 $\sqrt{x^{3}}$ ）′=3 $\sqrt{x}$ C、（cos60°）′=﹣sin60° D、[ln（2x）]′= $\frac{1}{2 x}$

查看试题解析
4. 已知随机变量X的概率分布列如表所示：且X的数学期望EX=6，则（　　）
X
5
6
7
8
p
0.4
a
b
0.1

A、a=0.3，b=0.2 B、a=0.2，b=0.3 C、a=0.4，b=0.1 D、a=0.1，b=0.4

查看试题解析
5. 已知自然数x满足3A $_{x + 1}^{3}$ ﹣2A $_{x + 2}^{2}$ =6A $_{x + 1}^{2}$ ，则x（）

A、3 B、5 C、4 D、6

查看试题解析
6. 如图所示，在正方体ABCD﹣A₁B₁C₁D₁中，已知棱长为a，M，N分别是BD和AD的中点，则B₁M与D₁N所成角的余弦值为（）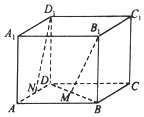

A、﹣ $\frac{\sqrt{15}}{15}$ B、 $\frac{\sqrt{30}}{10}$ C、﹣ $\frac{\sqrt{30}}{10}$ D、 $\frac{\sqrt{15}}{15}$

查看试题解析
7. 以下三个命题
①设回归方程为 $\hat{y}$ =3﹣3x，则变量x增加一个单位时，y平均增加3个单位；
②两个随机变量的线性相关性越强，则相关系数的绝对值越接近于1；
③在某项测量中，测量结果ξ服从正态分布N （1，σ²）（σ＞0）．若ξ在（0，1）内取值的概率为0.4，则ξ在（0，2）内取值的概率为0.8．
其中真命题的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 高考来临之际，食堂的伙食进行了全面升级．某日5名同学去食堂就餐，有米饭，花卷，包子和面条四种主食，每种主食均至少有一名同学选择且每人只能选择其中一种．花卷数量不足仅够一人食用，则不同的食物搭配方案种数为（）

A、132 B、180 C、240 D、600

查看试题解析
9. 某企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系，随机抽取了72名员工进行调查，所得的数据如表所示：
积极支持改革
不太支持改革
合    计
工作积极
28
8
36
工作一般
16
20
36
合    计
44
28
72
对于人力资源部的研究项目，根据上述数据能得出的结论是
（参考公式与数据： $X^{2} = \frac{n {(n_{11} n_{22} - n_{12} n_{21})}^{2}}{n_{1} + n_{2} + n_{1} + n_{2}}$ ．当Χ²＞3.841时，有95%的把握说事件A与B有关；当Χ²＞6.635时，有99%的把握说事件A与B有关；当Χ²＜3.841时认为事件A与B无关．）（   ）

A、有99%的把握说事件A与B有关 B、有95%的把握说事件A与B有关 C、有90%的把握说事件A与B有关 D、事件A与B无关

查看试题解析
10. 某个部件由三个元件按图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作（其中元件1，2，3正常工作的概率都为 $\frac{1}{2}$ ），设三个电子元件的使用寿命（单位：小时）均服从正态分布N（1000，50²），且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为（）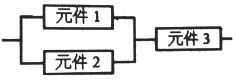

A、 $\frac{3}{4}$ B、 $\frac{1}{4}$ C、 $\frac{5}{8}$ D、 $\frac{3}{8}$

查看试题解析
11. 若（1+2x）⁶=a₀+a₁x+a₂x²+a₃x³+a₄x⁴+a₅x⁵+a₆x⁶ ，则a₀+a₁+a₃+a₅=（）

A、364 B、365 C、728 D、730

查看试题解析
12. 把标号为1，2，3，4，5的五个小球全部放入标号为1，2，3，4的四个盒子中，不许有空盒且任意一个小球都不能放入标有相同标号的盒子中，则不同的方法种数是（）

A、36 B、48 C、60 D、84

查看试题解析

二、填空题：

13. 已知A（1，0，0），B（0，1，0），C（0，0，1），则平面ABC的一个单位法向量是．

查看试题解析
14. 某校组织10名学生参加高校的自主招生活动，其中6名男生，4名女生，根据实际要从10名同学中选3名参加A校的自主招生，则其中恰有1名女生的概率是．

查看试题解析
15. ∠AOB在平面α内，OC是平面α的一条斜线，若已知∠AOB=∠BOC=∠COA=60°，则OC与平面α所成的角的余弦值等于．

查看试题解析
16. 将三项式（x²+x+1）ⁿ展开，当n=0，1，2，3，…时，得到以下等式：
（x²+x+1）⁰=1
（x²+x+1）¹=x²+x+1
（x²+x+1）²=x⁴+2x³+3x²+2x+1
（x²+x+1）³=x⁶+3x⁵+6x⁴+7x³+6x²+3x+1
…
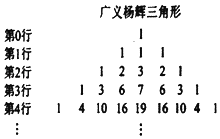
观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数（不足3数的，缺少的数计为0）之和，第k行共有2k+1个数．若在（1+ax）（x²+x+1）⁵的展开式中，x⁸项的系数为67，则实数a值为．

查看试题解析

三、解答題：

17. 已知，f（x）=1﹣lnx﹣ $\frac{1}{8}$ x²

(1)、求曲线f（x）在x=1处的切线方程；

(2)、求曲线f（x）的切线的斜率及倾斜角α的取值范围．

查看试题解析
18. 在棱长为2的正方体ABCD﹣A₁B₁C₁D₁中，E是BC的中点，F是DD₁的中点，

(1)、求证：CF∥平面A₁DE；

(2)、求二面角A₁﹣DE﹣A的余弦值．

查看试题解析
19. 已知（ $\sqrt{x}$ + $\frac{2}{x^{2}}$ ）ⁿ的展开式中，第五项与第七项的二项式系数相等．
（I ）求该展开式中所有有理项的项数；
（II）求该展开式中系数最大的项．

查看试题解析
20. 某班有6名班干部，其中男生4人，女生2人，任选3人参加学校组织的义务植树活动．

（I）求男生甲、女生乙至少有1人被选中的概率；
（II）设“男生甲被选中”为事件A，“女生乙被选中”为事件B，求P （A）和P （B|A）．

查看试题解析
21. 如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，AB=2，AD= $\sqrt{3}$ ，∠DAB= $\frac{π}{6}$ ，PD⊥AD，PD⊥DC．
（Ⅰ）证明：BC⊥平面PBD；
（Ⅱ）若二面角P﹣BC﹣D为 $\frac{π}{3}$ ，求AP与平面PBC所成角的正弦值．

查看试题解析
22. 某校设计了一个实验考察方案：考生从6道备选题中随机抽取3道题，按照题目要求独立完成全部实验操作，规定：至少正确完成其中的2道题便可通过．已知6道备选题中考生甲有4道能正确完成，2道题不能完成；考生乙每题正确完成的概率都是 $\frac{2}{3}$ ，且每题正确完成与否互不影响．
（I）求甲考生通过的概率；
（II）求甲、乙两考生正确完成题数的概率分布列，和甲、乙两考生的数学期望；
（Ⅲ）请分析比较甲、乙两考生的实验操作能力．

查看试题解析

	积极支持改革	不太支持改革	合计
工作积极	28	8	36
工作一般	16	20	36
合计	44	28	72

X	5	6	7	8
p	0.4	a	b	0.1