2016-2017学年湖北省孝感市七校联考高二下学期期中数学试卷（理科）

试卷更新日期：2017-05-19 类型：期中考试

进入出卷网下载

一、选择题：

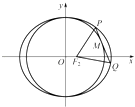
1. “两个三角形全等”是“两个三角形面积相等”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
2. 命题“∃x₀∈（0，+∞），lnx₀=x₀﹣1”的否定是（　　）

A、∃x₀∈（0，+∞），lnx₀≠x₀﹣1 B、∃x₀∉（0，+∞），lnx₀=x₀﹣1 C、∀x∈（0，+∞），lnx≠x﹣1 D、∀x∉（0，+∞），lnx=x﹣1

查看试题解析
3. 下列选项中说法错误的是（）

A、27是3的倍数或27是9的倍数 B、平行四边形的对角线互相垂直且平分 C、平行四边形的对角线互相垂直或平分 D、1是方程x﹣1=0的根，且是方程x²﹣5x+4=0的根

查看试题解析
4. 对于椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ ，下面说法正确的是（）

A、长轴长为2 B、短轴长为3 C、离心率为 $\frac{1}{2}$ D、焦距为1

查看试题解析
5. 已知向量 $a (2 ， - 3 ， 1) ， b = (- 4 ， 2 ， x)$ ，且 $a ⊥ b$ ，则x的值为（）

A、12 B、10 C、﹣14 D、14

查看试题解析
6. 若椭圆经过原点，且焦点为F₁（1，0）F₂（3，0），则其离心率为（）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
7. 过点M（﹣2，0）的直线l与椭圆x²+2y²=4交于P₁ ， P₂两点，设线段P₁P₂的中点为P．若直线l的斜率为k₁（k₁≠0），直线OP的斜率为k₂ ，则k₁k₂等于（）

A、﹣2 B、2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
8. 点M，N分别是正方体ABCD﹣A₁B₁C₁D₁的棱BB₁和B₁C₁的中点，则MN和CD₁所成角的大小为（）

A、30° B、60° C、90° D、120°

查看试题解析
9. 椭圆 $\frac{x^{2}}{4} + y^{2} = 1$ 的两个焦点为F₁、F₂ ，过F₁作垂直于x轴的直线与椭圆相交，一个交点为P，则P到F₂的距离为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{3}$ C、 $\frac{7}{2}$ D、4

查看试题解析
10. 如图，过抛物线y²=2px（p＞0）焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为（）

A、y²=3x B、y²=9x C、y²= $\frac{3}{2}$ x D、y²= $\frac{9}{2}$ x

查看试题解析
11. 双曲线 $\frac{x^{2}}{m} - \frac{y^{2}}{n} = 1 (m > 0 ， n > 0)$ 和椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 有相同的焦点F₁ ， F₂ ， M为两曲线的交点，则|MF₁|•|MF₂|等于（）

A、a+m B、b+m C、a﹣m D、b﹣m

查看试题解析
12. 已知 $a = (2 ， t ， t) ， b = (1 - t ， 2 t - 1 ， 0)$ ，则 $| b - a |$ 的最小值是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、 $\sqrt{6}$

查看试题解析

二、填空题：

13. 特称命题“有些三角形的三条中线相等”的否定是．

查看试题解析
14. 在一次射击训练中，某战士连续射击了两次．设命题p是“第一次射击击中目标”，q是“第二次击中目标”．则用p，q以及逻辑联结词（￢，∧，∨）表示“两次都没有击中目标”为．

查看试题解析
15. 若抛物线y²=4x上的点M到焦点的距离为10，则M到y轴的距离是

查看试题解析
16. 已知向量 $a, b, c$ 是空间的一个单位正交基底，向量 $a + b, a - b, c$ 是空间的另一个基底．若向量 $m$ 在基底 $a, b, c$ 下的坐标为（1，2，3），则 $m$ 在基底 $a + b, a - b, c$ 下的坐标为．

查看试题解析

三、解答题：

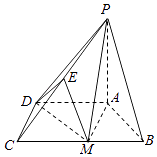
17. 证明：a²+b²+c²=ab+bc+ca的充要条件是△ABC为等边三角形．这里a，b，c是△ABC的三条边．

查看试题解析
18. 已知a∈R，设命题p：指数函数y=a^x（a＞0且a≠1）在R上单调递增；命题q：函数y=ln（ax²﹣ax+1）的定义域为R，若“p且q”为假，“p或q”为真，求a的取值范围．

查看试题解析
19. 如图，线段AB在平面α内，线段BD⊥AB，线段AC⊥α，且AB= $\frac{7}{2}$ ，AC=BD=12，CD= $\frac{25}{2}$ ，求线段BD与平面α所成的角．

查看试题解析
20. 如图，已知直线与抛物线y²=2px（p＞0）交于A，B两点，且OA⊥OB，OD⊥AB交AB于点D（不为原点）．
（Ⅰ）求点D的轨迹方程；
（Ⅱ）若点D坐标为（2，1），求p的值．

查看试题解析
21. 已知四棱锥P﹣ABCD，底面ABCD是直角梯形，AD∥BC，∠BCD=90°，PA⊥底面ABCD，△ABM是边长为2的等边三角形， $P A = D M = 2 \sqrt{3}$ ．
（Ⅰ）求证：平面PAM⊥平面PDM；
（Ⅱ）若点E为PC中点，求二面角P﹣MD﹣E的余弦值．

查看试题解析
22. 已知椭圆 $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的右焦点为F₂（1，0），点H（2， $\frac{2 \sqrt{10}}{3}$ ）在椭圆上．

(1)、求椭圆的方程；

(2)、点M在圆x²+y²=b²上，且M在第一象限，过M作圆x²+y²=b²的切线交椭圆于P，Q两点，问：△PF₂Q的周长是否为定值？如果是，求出定值；如果不是，说明理由．

查看试题解析