2016-2017学年湖北省鄂东南省级示范高中联考高二下学期期中数学试卷（理科）

试卷更新日期：2017-05-19 类型：期中考试

进入出卷网下载

一、选择题

1. 命题“∃x₀＞0，使得（x₀+1） $e^{x_{0}}$ ＞1”的否定是（）

A、∀x＞0，总有（x+1）e^x≤1 B、∀x≤0，总有（x+1）e^x≤1 C、∃x₀≤0，总有（x₀+1） $e^{x_{0}}$ ≤1 D、∃x₀＞0，使得（x₀+1） $e^{x_{0}}$ ≤1

查看试题解析
2. 为了解城市居民的健康状况，某调查机构从一社区的120名年轻人，80名中年人，60名老年人中，用分层抽样方法抽取了一个容量为n的样本进行调查，其中老年人抽取了3名，则n=（）

A、26 B、24 C、20 D、13

查看试题解析
3. 为了解重庆某社区居民的家庭年收入和年支出的关系，随机调查了5户家庭，得到统计数据表，根据表中可得回归直线方程 $\hat{y}$ = $\hat{b}$ x+ $\hat{a}$ ，其中 $\hat{b}$ =0.5，据此估计，该社区一户收入为16万元家庭年支出为（）
收入x（万元）
6
8
10
12
14
支出y（万元）
6
7
8
9
10

A、15万元 B、14万元 C、11万元 D、10万元

查看试题解析
4. 某地区教学考试的成绩X～N（100，100），成绩X位于区间（110，120]的概率是（）

参考数据
P（μ﹣σ＜X≤μ+σ）=0.6826
P（μ﹣2σ＜X≤μ+2σ）=0.9544
P（μ﹣3σ＜X≤μ+3σ）=0.9974．

A、0.6826 B、0.9544 C、0.2718 D、0.1359

查看试题解析
5. 已知正方体ABCD﹣A₁B₁C₁D₁的各顶点都在球O表面上，在球O内任取一点M，则点M在正方体ABCD﹣A₁B₁C₁D₁内的概率是（）

A、 $\frac{3 \sqrt{2}}{4 π}$ B、 $\frac{3 \sqrt{2}}{2 π}$ C、 $\frac{\sqrt{3}}{3 π}$ D、 $\frac{2 \sqrt{3}}{3 π}$

查看试题解析
6. 某市政府在调查市民收入增减与旅游愿望的关系时，采用独立性检验法抽查了3000人，计算发现K²的观测者k=6.023，根据这一数据查阅如表：
P（K²≥k₀）
0.50
0.40
0.25
0.15
0.10
0.5
0.025
0.010
0.005
0.001
K₀
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
得到的正确结论是（）

A、有97.5%以上的把握认为“市民收入增减与旅游愿望无关” B、有97.5%以上的把握认为“市民收入增减与旅游愿望有关” C、在犯错误的概率不超过0.25%的前提下，认为“市民收入增减与旅游愿望无关” D、在犯错误的概率不超过0.25%的前提下，认为“市民收入增减与旅游愿望有关”

查看试题解析
7. 执行如图所示的程序框图，若输出的S=88，则判断框内应填入的条件是（）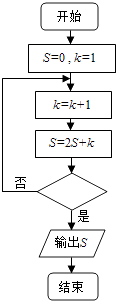

A、k＞7 B、k＞6 C、k＞5 D、k＞4

查看试题解析
8. 在三棱柱ABC﹣A₁B₁C₁中，各侧面均为正方形，侧面AA₁C₁C的对角线相交于点M，则BM与平面ABC所成角的大小是（）

A、30° B、45° C、60° D、90°

查看试题解析
9. 高二（7）班参加冬令营的6位同学排成一排照相，甲乙必须相邻且甲、乙、丙必须从左到右的排法种数为（）

A、120 B、60 C、36 D、72

查看试题解析
10. 若函数f（x）在R上可导，且f（x）=x²+2f′（1）x+3，则（）

A、f（0）＜f（4） B、f（0）=f（4） C、f（0）＞f（4） D、无法确定

查看试题解析
11. 已知（1﹣x）¹⁰=a₀+a₁（1+x）+a₂（1+x）²+…+a₁₀（1+x）¹⁰ ，则a₉=（）

A、﹣20 B、20 C、﹣10 D、10

查看试题解析
12. 已知点P是双曲线 $\frac{x^{2}}{36}$ ﹣ $\frac{y^{2}}{64}$ =1的右支上一点，F₁、F₂分别为双曲线的左、右焦点，I为△PF₁F₂的内心，若 $S_{△ I P F_{1}}$ = $S_{△ I P F_{2}}$ +λ $S_{△ I F_{1} F_{2}}$ 成立，则λ的值为（）

A、 $\frac{5}{8}$ B、 $\frac{4}{5}$ C、 $\frac{3}{5}$ D、 $\frac{3}{4}$

查看试题解析

二、填空题

13. 已知P（A）= $\frac{2}{5}$ ，P（AB）= $\frac{1}{3}$ ，则P（B|A）= ．

查看试题解析
14. 如图某综艺节目现场设有A，B，C，D四个观众席，现有由5不同颜色的马甲可供现场观众选择，同一观众席上的马甲的颜色相同，相邻观众席上的马甲的颜色不相同，则不同的安排方法种数为．

查看试题解析
15. 某大厦有一部电梯，若该电梯在底层有5个乘客，且每位乘客在第10层下电梯的概率为 $\frac{1}{3}$ ，用ξ表示5位乘客在第10层下电梯的人数，则随机变量ξ的期望E（ξ）= ．

查看试题解析
16. 以下几个命题中真命题的序号为．

①在空间中，m、n是两条不重合的直线，α、β是两个不重合的平面，如果α⊥β，α∩β=n，m⊥n，那么m⊥β；
②相关系数r的绝对值越接近于1，两个随机变量的线性相关性越强；
③用秦九昭算法求多项式f（x）=208+9x²+6x⁴+x⁶在x=﹣4时，v₂的值为22；
④过抛物线y²=4x的焦点作直线与抛物线相交于A、B两点，则使它们的横坐标之和等于4的直线有且只有两条．

查看试题解析

三、解答题

17. 已知集合A是函数y=lg（6+5x﹣x²）的定义域，集合B是不等式x²﹣2x+1﹣a²≥0（a＞0）的解集．p：x∈A，q：x∈B．

(1)、若A∩B=∅，求a的取值范围；

(2)、若￢p是q的充分不必要条件，求a的取值范围．

查看试题解析
18. 如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩（均为整数）的频率分布直方图，该直方图恰好缺少了成绩在区间[70，80）内的图形，根据图形的信息，回答下列问题：

(1)、求成绩在区间[70，80）内的频率，并补全这个频率分布直方图，并估计这次考试的及格率（60分及以上为及格）；

(2)、从成绩在[80，100]内的学生中选出三人，记在90分以上（含90分）的人数为X，求X的分布列及数学期望．

查看试题解析
19. 已知函数f（x）=ax³+bx²+cx在x=±1处取得极值，且在x=0处的切线的斜率为﹣3．

(1)、求f（x）的解析式；

(2)、求过点A（2，2）的切线方程．

查看试题解析
20. 如图，在四棱锥P﹣ABCD中，底面ABCD是平行四边形，PA⊥底面ABCD，AB⊥AC，AB=1，BC=2，PA= $\frac{\sqrt{2}}{2}$ ，E为BC的中点．

(1)、证明：PE⊥ED；

(2)、求二面角E﹣PD﹣A的大小．

查看试题解析
21.
已知椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0），短轴长2，两焦点分别为F₁ ， F₂ ，过F₁的直线交椭圆C于M，N两点，且△F₂MN的周长为8．

(1)、求椭圆C的方程；

(2)、直线l与椭圆C相交于A，B点，点D为椭圆C上一点，四边形AOBD为矩形，求直线l的方程．

查看试题解析
22. 已知函数f（x）=lnx+x²﹣ax（a∈R）

(1)、a=3时，求函数f（x）的单调区间；

(2)、若f（x）≤2x²恒成立，求实数a的取值范围；

(3)、求证；lnn＞ $\frac{1}{3}$ + $\frac{1}{5}$ +1 $\frac{1}{7}$ +…+ $\frac{1}{2 n - 1}$ （n∈N⁺）且n≥2．

查看试题解析

P（K²≥k₀）	0.50	0.40	0.25	0.15	0.10	0.5	0.025	0.010	0.005	0.001
K₀	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

收入x（万元）	6	8	10	12	14
支出y（万元）	6	7	8	9	10