辽宁省抚顺市2019届高三文数第一次模拟考试试卷

试卷更新日期：2019-05-15 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知复数 $z = \frac{3}{1 - 2 i}$ （ $i$ 是虚数单位），则 $\bar{z} =$ （）

A、 $\frac{3}{5} + \frac{6}{5} i$ B、 $\frac{3}{5} - \frac{6}{5} i$ C、 $\frac{1}{5} - \frac{2}{5} i$ D、 $\frac{1}{5} + \frac{2}{5} i$

查看试题解析
2. 已知集合 $A = {x \in Z | 0 < x < 4}$ ， $B = {x | (x + 1) (x - 2) < 0}$ ，则 $A \cap^{} B =$ （）

A、 $(0, 2)$ B、 $(- 1, 2)$ C、 ${0, 1}$ D、 ${1}$

查看试题解析
3. 在等差数列 ${a_{n}}$ 中，前 $n$ 项和 $S_{n}$ 满足 $S_{9} - S_{2} = 35$ ，则 $a_{6}$ 的值是（）

A、5 B、7 C、9 D、3

查看试题解析
4. 军训时，甲、乙两名同学进行射击比赛，共比赛10场，每场比赛各射击四次，且用每场击中环数之和作为该场比赛的成绩．数学老师将甲、乙两名同学的10场比赛成绩绘成如图所示的茎叶图，并给出下列4个结论：(1)甲的平均成绩比乙的平均成绩高；(2)甲的成绩的极差是29；(3)乙的成绩的众数是21；(4)乙的成绩的中位数是18．则这4个结论中，正确结论的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 已知向量 $\overset{⇀}{a} = (1, 2 \sqrt{2})$ ， $| \overset{⇀}{b} | = 1$ ，向量 $\overset{⇀}{a}$ 与 $\overset{⇀}{b}$ 的夹角为 $120 °$ ，则 $| \overset{⇀}{a} + \overset{⇀}{b} |$ 的值为（）

A、 $\sqrt{13}$ B、 $\sqrt{7}$ C、7 D、13

查看试题解析
6. 实数 $x$ ， $y$ 满足约束条件 ${\begin{matrix} x + 2 y - 2 \leq 0 \\ x - y + 1 \geq 0 \\ x - 2 y - 2 \leq 0 \end{matrix}$ ，则 $z = 2 x - y$ 的最小值是（）

A、5 B、4 C、 $- 5$ D、 $- 6$

查看试题解析
7. 某几何体的三视图如图所示，则该几何体的体积为（）

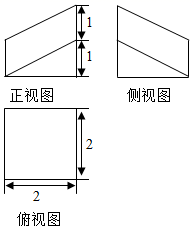A、2 B、4 C、6 D、8

查看试题解析
8. 执行如图的程序框图，则输出的 $S$ 的值是（）

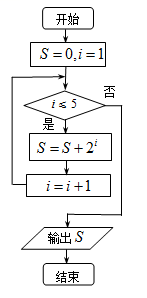A、30 B、126 C、62 D、 $- 126$

查看试题解析
9. 学校根据课程计划拟定同时实施“科普之旅”和“红色之旅”两个主题的研学旅行，现在小芳和小敏都已经报名参加此次的研学旅行，则两人选择的恰好是同一研学旅行主题的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{3}{4}$

查看试题解析
10. 在三棱锥 $P - A B C$ 中，已知 $P A = A B = A C$ ， $∠ B A C = ∠ P A C$ ，点 $D$ ， $E$ 分别为棱 $B C$ ， $P C$ 的中点，则下列结论正确的是（）

A、直线 $D E ⊥$ 直线 $A D$ B、直线 $D E ⊥$ 直线 $P A$ C、直线 $D E ⊥$ 直线 $A B$ D、直线 $D E ⊥$ 直线 $A C$

查看试题解析
11. 已知斜率为 $- 1$ 的直线过抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点，且与该抛物线交于 $A$ ， $B$ 两点，若线段 $A B$ 的中点的纵坐标为 $- 2$ ，则该抛物线的准线方程为（）

A、 $x = 2$ B、 $x = 1$ C、 $x = - 2$ D、 $x = - 1$

查看试题解析
12. 若函数 $f (x) = x ln x - x^{3} + x^{2} - a x$ 有两个不同的零点，则实数 $a$ 的取值范围是（）

A、 $(0 ， + \infty)$ B、 $(0 ， 1]$ C、 $[- 1 ， 0)$ D、 $(- \infty ， 0)$

查看试题解析

二、填空题

13. 已知函数 $f (x)$ 是奇函数，且当 $x < 0$ 时 $f (x) = {(\frac{1}{2})}^{x}$ ，则 $f (3)$ 的值是．

查看试题解析
14. 若 $sin (α - \frac{3}{2} π) = \frac{3}{5}$ ，则 $cos 2 α$ 的值是．

查看试题解析
15. 在平面直角坐标系 $x O y$ 中，过 $x$ 轴上的点 $P$ 作双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的一条渐近线的垂线，垂足为 $M$ ，若 $O M = \sqrt{6}$ ， $P M = \sqrt{3}$ ，则双曲线 $C$ 的离心率的值是．

查看试题解析
16. 各项为正数的等比数列 ${a_{n}}$ 中， $a_{2}$ 与 $a_{10}$ 的等比中项为 $\frac{\sqrt{3}}{3}$ ,则 ${log}_{3} a_{4} + {log}_{3} a_{8} =$ ．

查看试题解析

三、解答题

17. 已知 $a$ ， $b$ ， $c$ 分别是 $Δ A B C$ 的三个内角 $A$ ， $B$ ， $C$ 的对边，若 $a = 10$ ，角 $B$ 是最小的内角，且 $3 c = 4 a sin B + 3 b cos A$ ．
（Ⅰ）求 $sin B$ 的值；

（Ⅱ）若 $c = 14$ ，求 $b$ 的值．

查看试题解析
18. “微信运动”是手机 $A P P$ 推出的多款健康运动软件中的一款，大学生M的微信好友中有400位好友参与了“微信运动”．他随机抽取了40位参与“微信运动”的微信好友（女20人，男20人）在某天的走路步数，经统计，其中女性好友走路的步数情况可分为五个类别： $A$ 、 $0 \sim 2000$ 步，（说明：“ $0 \sim 2000$ ”表示大于或等于0，小于2000，以下同理）， $B$ 、 $2000 \sim 5000$ 步， $C$ 、 $5000 \sim 8000$ 步， $D$ 、 $8000 \sim 10000$ 步， $E$ 、 $10000 \sim 12000$ 步，且 $A$ 、 $B$ 、 $C$ 三种类别的人数比例为 $1 ： 4 ： 3$ ，将统计结果绘制如图所示的柱形图；男性好友走路的步数数据绘制如图所示的频率分布直方图．

（Ⅰ）若以大学生 $M$ 抽取的微信好友在该天行走步数的频率分布，作为参与“微信运动”的所有微信好友每天走路步数的概率分布，试估计大学生 $M$ 的参与“微信运动”的400位微信好友中，每天走路步数在 $2000 \sim 8000$ 的人数；

（Ⅱ）若在大学生 $M$ 该天抽取的步数在 $8000 \sim 10000$ 的微信好友中，按男女比例分层抽取6人进行身体状况调查，然后再从这6位微信好友中随机抽取2人进行采访，求其中至少有一位女性微信好友被采访的概率．

查看试题解析
19. 如图，在正三棱柱 . 中， $A B = A A_{1} = 2$ ， $E$ ， $F$ 分别为 $A B$ ， $B_{1} C_{1}$ 的中点．

（Ⅰ）求证： $B_{1} E ∕ ∕$ 平面 $A C F$ ；

（Ⅱ）求三棱锥 $B_{1} - A C F$ 的体积．

查看试题解析
20. 已知点 $M (2 ， 1)$ 在椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 上， $A$ ， $B$ 是长轴的两个端点，且 $\overset{⇀}{M A} \cdot \overset{⇀}{M B} = - 3$ ．

（Ⅰ）求椭圆 $C$ 的标准方程；

（Ⅱ）已知点 $E (1 ， 0)$ ，过点 $M (2 ， 1)$ 的直线 $l$ 与椭圆的另一个交点为 $N$ ，若点 $E$ 总在以 $M N$ 为直径的圆内，求直线 $l$ 的斜率的取值范围．

查看试题解析
21. 已知函数： $f (x) = lnx - a x - 3 (a \neq 0)$ ．
（Ⅰ）讨论函数 $f (x)$ 的单调性；

（Ⅱ）若函数 $f (x)$ 有最大值 $M$ ，且 $M > a - 5$ ，求实数 $a$ 的取值范围．

查看试题解析
22. 在直角坐标系 $x O y$ 中，以坐标原点 $O$ 为极点， $x$ 轴的正半轴为极轴建立极坐标系，已知曲线 $C_{1}$ 的极坐标方程为 $ρ = 2 sin θ$ ，直线 $l$ 的参数方程为 ${\begin{matrix} x = \frac{1}{2} t \\ y = \frac{\sqrt{3}}{2} t + 2 \end{matrix}$ （ $t$ 为参数）．
（Ⅰ）求曲线 $C_{1}$ 的参数方程和直线 $l$ 的直角坐标方程；

（Ⅱ）设 $D$ 为曲线 $C_{1}$ 上在第二象限内的点，且在点 $D$ 处的切线与直线 $l$ 平行，求点 $D$ 的直角坐标．

查看试题解析
23. 已知函数 $f (x) = | x + a | + | x - \frac{1}{a} |$ ．
（Ⅰ）当 $a = 1$ 时，解不等式 $f (x) \geq 5$ ；

（Ⅱ）若 $\forall x \in R$ ， $f (x) \geq | m - 1 |$ 恒成立，求实数 $m$ 的取值范围．

查看试题解析