河北省唐山市2019届高三理数第二次模拟考试试卷
试卷更新日期:2019-05-15 类型:高考模拟
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 已知复数 满足 ,则 的共轭复数为( )A、 B、 C、 D、3. 在等差数列 中, , ,则 ( )A、10 B、12 C、14 D、164. 已知角 的顶点为坐标原点,始边与 轴的非负半轴重合,终边上一点 ,则 ( )A、 B、 C、 D、5. 已知双曲线 : 的焦距为4, 为 上一点,则 的渐近线方程为( )A、 B、 C、 D、6. 已知直线 , 和平面 , ,有如下三个命题:
①若存在平面 ,使 , ,则 ;②若 , 是两条异面直线, , , , ,则 ;③若 , , ,则 .其中正确命题的个数是( )
A、0 B、1 C、2 D、37. 已知函数 的最小正周期为 ,把 的图像向左平移 个单位后,所得函数图象的一条对称轴为( )A、 B、 C、 D、8. 已知函数 为奇函数,则 在 处的切线斜率等于( )A、6 B、-2 C、-6 D、-89. 某几何体的三视图如图所示,则该几何体的表面积为( ) A、 B、 C、 D、10. 割补法在我国古代数学著作中称为“出入相补”,刘徽称之为“以盈补虚”,即以多余补不足,是数量的平均思想在几何上的体现.如图揭示了刘徽推导三角形面积公式的方法.在 内任取一点,则该点落在标记“盈”的区域的概率为( )
A、 B、 C、 D、10. 割补法在我国古代数学著作中称为“出入相补”,刘徽称之为“以盈补虚”,即以多余补不足,是数量的平均思想在几何上的体现.如图揭示了刘徽推导三角形面积公式的方法.在 内任取一点,则该点落在标记“盈”的区域的概率为( )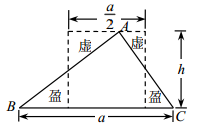 A、 B、 C、 D、11. 已知抛物线 : 的焦点为 ,点 在 上,以 为半径的圆 与 轴交于 , 两点, 为坐标原点,若 ,则圆 的半径 ( )A、2 B、3 C、4 D、512. 已知 , , ,则 , , 的大小关系是( )A、 B、 C、 D、
A、 B、 C、 D、11. 已知抛物线 : 的焦点为 ,点 在 上,以 为半径的圆 与 轴交于 , 两点, 为坐标原点,若 ,则圆 的半径 ( )A、2 B、3 C、4 D、512. 已知 , , ,则 , , 的大小关系是( )A、 B、 C、 D、二、填空题
-
13. 已知向量 , 满足 , ,且 ,则 .14. 设变量 , 满足约束条件 ,则 的最大值为 .15. 将六名教师分配到甲、乙、丙、丁四所学校任教,其中甲校至少分配两名教师,其它三所学校至少分配一名教师,则不同的分配方案共有种.(用数字作答)16. 各项均为正数的数列 满足 , ,则 .
三、解答题
-
17. 在 中,角 , , 的对边分别为 , , , .(1)、求角 ;(2)、若 , ,求 .18. 如图,在边长为8的菱形 中, ,将 沿 折起,使点 到达 的位置,且二面角 为 .
 (1)、求异面直线 与 所成角的大小;(2)、若点 为 中点,求直线 与平面 所成角的正弦值.19. 苹果可按果径 (最大横切面直径,单位: .)分为五个等级: 时为1级, 时为2级, 时为3级, 时为4级, 时为5级.不同果径的苹果,按照不同外观指标又分为特级果、一级果、二级果.某果园采摘苹果10000个,果径 均在 内,从中随机抽取2000个苹果进行统计分析,得到如图1所示的频率分布直方图,图2为抽取的样本中果径在80以上的苹果的等级分布统计图.
(1)、求异面直线 与 所成角的大小;(2)、若点 为 中点,求直线 与平面 所成角的正弦值.19. 苹果可按果径 (最大横切面直径,单位: .)分为五个等级: 时为1级, 时为2级, 时为3级, 时为4级, 时为5级.不同果径的苹果,按照不同外观指标又分为特级果、一级果、二级果.某果园采摘苹果10000个,果径 均在 内,从中随机抽取2000个苹果进行统计分析,得到如图1所示的频率分布直方图,图2为抽取的样本中果径在80以上的苹果的等级分布统计图.
附:若随机变量 服从正态分布 ,则
, , .
(1)、假设 服从正态分布 ,其中 的近似值为果径的样本平均数 (同一组数据用该区间的中点值代替), ,试估计采摘的10000个苹果中,果径 位于区间 的苹果个数;(2)、已知该果园今年共收获果径在80以上的苹果 ,且售价为特级果12元 ,一级果10元 ,二级果9元 .设该果园售出这 苹果的收入为 ,以频率估计概率,求 的数学期望.20. 已知 , ,当 , 分别在 轴, 轴上滑动时,点 的轨迹记为 .(1)、求曲线 的方程;(2)、设斜率为 的直线 与 交于 , 两点,若 ,求 .