东北三省四市2019届高三理数第一次考试试卷
试卷更新日期:2019-05-15 类型:高考模拟
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 在复平面内,表示复数 的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列各点中,可以作为函数 图象的对称中心的是( )A、 B、 C、 D、4. 执行如图所示的程序框图,如果输入 ,则输出p为( )
 A、6 B、24 C、120 D、7205. 已知等差数列 的前n项和为 ,且 ,则 =( )A、0 B、10 C、15 D、306. 已知 为两条不重合直线, 为两个不重合平面,下列条件中, 的充分条件是( )A、 B、 C、 D、7. “科技引领,布局未来”科技研发是企业发展的驱动力量。 年,某企业连续 年累计研发投入搭 亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这 年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
A、6 B、24 C、120 D、7205. 已知等差数列 的前n项和为 ,且 ,则 =( )A、0 B、10 C、15 D、306. 已知 为两条不重合直线, 为两个不重合平面,下列条件中, 的充分条件是( )A、 B、 C、 D、7. “科技引领,布局未来”科技研发是企业发展的驱动力量。 年,某企业连续 年累计研发投入搭 亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这 年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( ) A、 年至 年研发投入占营收比增量相比 年至 年增量大 B、 年至 年研发投入增量相比 年至 年增量小 C、该企业连续 年研发投入逐年增加 D、该企业来连续 年来研发投入占营收比逐年增加8. 已知 是两个单位向量,且夹角为 ,则 与 数量积的最小值为( )A、 B、 C、 D、9. 我国古代数学名著《九章算术·商功》中阐述:“斜解立方,得两壍堵。斜解壍堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,则对该几何体描述:
A、 年至 年研发投入占营收比增量相比 年至 年增量大 B、 年至 年研发投入增量相比 年至 年增量小 C、该企业连续 年研发投入逐年增加 D、该企业来连续 年来研发投入占营收比逐年增加8. 已知 是两个单位向量,且夹角为 ,则 与 数量积的最小值为( )A、 B、 C、 D、9. 我国古代数学名著《九章算术·商功》中阐述:“斜解立方,得两壍堵。斜解壍堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,则对该几何体描述:①四个侧面都是直角三角形;②最长的侧棱长为 ;③四个侧面中有三个侧面是全等的直角三角形;④外接球的表面积为 .其中正确的个数为( )
 A、0 B、1 C、2 D、310. 函数 的部分图象大致是( )A、
A、0 B、1 C、2 D、310. 函数 的部分图象大致是( )A、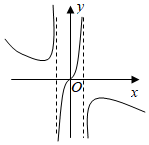 B、
B、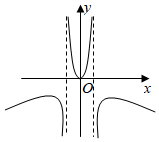 C、
C、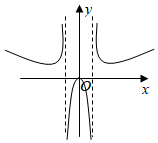 D、
D、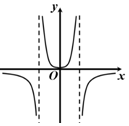 11. 已知抛物线 的焦点为 ,过 且倾斜角为 的直线与抛物线 交于 两点,若 的中点在 轴上的射影分别为 ,且 ,则抛物线 的准线方程为( )A、 B、 C、 D、12. 已知函数 ,若 ,且 ,则 的取值范围是( )A、 B、 C、 D、
11. 已知抛物线 的焦点为 ,过 且倾斜角为 的直线与抛物线 交于 两点,若 的中点在 轴上的射影分别为 ,且 ,则抛物线 的准线方程为( )A、 B、 C、 D、12. 已知函数 ,若 ,且 ,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 已知 ,若 依次成等比数列,则 的最小值为 .14. 已知矩形 ,以 为焦点,且过 两点的双曲线的离心率为 .15. 若8件产品中包含 件一等品,在其中任取 件,则在已知取出的 件中有 件不是一等品的条件下,另 件是一等品的概率为 .16. 已知数列 中, 则 .
三、解答题
-
17. 在 中
若 ,求 的面积;
若 ,求 的长.
18. 某工厂有甲,乙两个车间生产同一种产品,甲车间有工人 人,乙车间有工人 人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位: )进行统计,按照 进行分组,得到下列统计图.
分别估算两个车间工人中,生产一件产品时间少于 的人数
分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
从第一组生产时间少于 的工人中随机抽取 人,记抽取的生产时间少于 的工人人数为随机变量 ,求 的分布列及数学期望.
19. 如图,等腰梯形 中, , , 为 中点,将 沿 折到 的位置.
证明: ;
当四棱锥 的体积最大是,求二面角 的余弦值.
20. 已知椭圆 : 的短轴端点为 , ,点 是椭圆 上的动点,且不与 , 重合,点 满足 , .
(Ⅰ)求动点 的轨迹方程;
(Ⅱ)求四边形 面积的最大值.